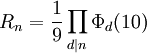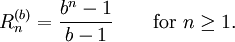Los repunits se definen matemáticamente como

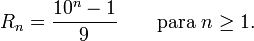Así, el número R_n consta de n ejemplares del dígito 1. La secuencia de repunits comienza 1, 11,  111, 1111,... (secuencia A002275 en OEIS).

Contenido 1 Historia 2 primos Repunit 3 Generalizaciones 3.1 Además 4 Referencias 5 Enlaces externos

Historia

Aunque no se conocían por ese nombre, repunits en base decimal fueron estudiados por muchos matemáticos durante el siglo XIX en un esfuerzo de desarrollar y predecir el modelo cíclico de los decimales recurrentes.^[1]

Se encontró tempranamente que para cualquier primo p mayor que 5, el período del decimal expansion de 1/p es igual al largo del número repunit menor que es divisible por p. Se han publicado tablas de periodos de recíprocos de primos hasta 60000 hacia 1860 y permitió factorización de enteros por matemáticos como Reuschle de todos los repunits hasta R₁₆ y superiores. Hacia 1880, aún R₁₇ ha sido factorizado^[2] y es curioso que, aunque Édouard Lucas mostró que ningún primo inferior a tres millones tenía período diecinueve, no hubo intento de demostrar un repunit para primalidad hasta inicios del siglo XX. El matemático norteamericano Oscar Hoppe probó que R₁₉ es primo en 1916^[3] y Lehmer y Kraitchik, en forma independiente, hallan R₂₃ primo en 1929.

No se registran ulteriores avances en el estudio de repunits hasta 1960s, hasta el advenimiento de las computadoras, que permitieron hallar nuevos factores de repunits llenando los vacíos o gaps en tablas previas de períodos primos. Se encontró por los años 60 que R₃₁₇ era un probable primo y se demostró 11 años más tarde, cuando R₁₀₃₁ se demostró el único posible primo repunit con menos que 10000 dígitos. Fue demostrado en 1986 como primo, pero la pesquiza para primos repunits adicionales en los siguientes décadas consistentemente falló. Sin embargo, hubo un desarrollo mayor side-development en el campo generalizado de repunits, que producían un número grande de primos nuevos y probables primos.

Desde 1999, se han hallado cuatro posibles primos repunits, pero es improbable que pueda probarse el carácter primo de cualquiera de ellos en un futuro previsible por su tamaño enorme.

primos Repunit

La definición de repunits fue motivada por las matemáticas recreativas buscando los factores primos de tales números.

Es fácil mostrar que si n es divisible por a, entonces R_n es divisible por R_a:

donde Φ_d is the d^th polinomial ciclotómico y d oscila más allá de los divisores de n. Para p primo, 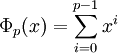, que pose una forma esperada de un repunit cuando x se substituye con 10.

Por ejemplo, 9 es divisible por 3, y ciertamente R₉ es divisible por R₃—in fact, 111111111 = 111 · 1001001. Los polinomios ciclotómicos correspondientes Φ₃(x) and Φ₉(x) are x² + x + 1 and x⁶ + x³ + 1 respectively. Así, para R_n sea primo n necesariamente debe ser primo. Pero no es suficiente para n sea primo; por ejemplo, R₃ = 111 = 3 · 37 no es primo. Excepto para este caso R₃, p puede sólo dividir R_n para primo n si p = 2kn + 1 para alguna k.

R_n es primo para n = 2, 19, 23, 317, 1031,... (sequence A004023 in OEIS). R₄₉₀₈₁ and R₈₆₄₅₃ son probablemente primos. A 3 de abril de 2007 Harvey Dubner (quien también encontró R₄₉₀₈₁) anunciado R₁₀₉₂₉₇ sea probablemente primo.^[4] He later announced there are no others from R₈₆₄₅₃ to R₂₀₀₀₀₀.^[5] On July 15 2007 Maksym Voznyy announced R₂₇₀₃₄₃ to be probably prime,^[6] along with his intent to search to 400000. Se ha conjeturado que existen infinitos primos repunit [1] y parece ocurrir groseramente tan a menudo como el prime number theorem prediciría: el exponente de Nth primo repunit es generalmente alrededor de un múltiplo fixed del exponente del (N-1)seimo.

Los primos repunits son un subconjunto trivial de los primos permutables, es decir, primos que permanecen primos despes de una permutación de sus dígitos.

Generalizaciones

Los matemáticos profesionales consideran a los repunits como una arbitrariedad, ya que este concepto depende del uso de numerales en base diez. Pero esa cualidad se puede evitar generalizando la idea a un repunit en base-b:

De hecho, la base-2 repunits son bien respetados números de Mersenne M_n = 2ⁿ − 1. El Proyecto de Cunningham debe a la documentación de factorización de enteros de (among other numbers) los repunits de base 2, 3, 5, 6, 7, 10, 11, y 12.

Ejemplo 1) el primero de los pocos primos base-3 repunit son 13, 1093, 797161, 3754733257489862401973357979128773, 6957596529882152968992225251835887181478451547013 (sequence A076481 in OEIS), corresponding to n of 3, 7, 13, 71, 103 (sequence A028491 in OEIS).

Ejemplo 2) el único primo repunit en base-4 es 5 (11₄), debido 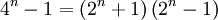, y 3 divide uno de estos, dejando los otros como un factor del repunit.

Es fácil prove que dado n, tales como n no es exactamente divisible por 2 o p, existe un repunit en base 2p que es un múltiplo de n.

Además

• Repdigit
• Número periódico
• polinomio todo en uno - otra generalización
• Goormaghtigh conjecture

Referencias

Enlaces externos

sitios de la Web

• The main tables of the Cunningham project.
• Repunit at The Prime Pages by Chris Caldwell.
• Repunits and their prime factors at World!Of Numbers.

Libros

• S. Yates, Repunits and repetends. ISBN 0-9608652-0-9.
• A. Beiler, Recreations in the theory of numbers. ISBN 0-486-21096-0. Chapter 11, of course.
• Paulo Ribenboim, The New Book Of Prime Number Records. ISBN 0-387-94457-5