La respuesta a impulso de un sistema simple de audio. Se muestra primero el impulso original, luego con las altas frecuencias reforzadas, y por último con las bajas frecuencias reforzadas.

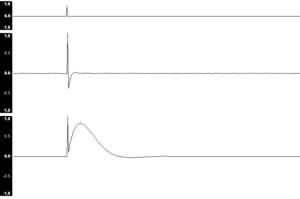
En términos simples, la respuesta a impulso o respuesta impulsiva de un sistema es la que se presenta en la salida frente a una señal muy breve, o impulso, en la entrada. Mientras que un impulso es un concepto difícil de imaginar, y es imposible en la realidad, éste representa el caso límite de un pulso infinítamente corto en el tiempo pero que mantiene su área o integral (por lo cual tiene un pico de amplitud infinitamente alto). Aunque es imposible en cualquier sistema real, es un concepto útil como idealización.

Bases matemáticas

Matemáticamente, un impulso puede ser representado por una función Delta de Dirac. Supongamos que T es un sistema discreto, es decir, que toma una entrada x[n] y produce una salida y[n]:

Por lo tanto T es un operador actuando sobre sucesiones (a través de los números enteros), produciendo nuevas sucesiones. Tener en cuenta que T no es el sistema, sino una representación matemática del sistema. T puede ser no lineal, por ejemplo:

o lineal, como:

.

Supongamos que T es lineal. Entonces

y

Supongamos también que T es invariante en el entorno, es decir que si entonces . En tal sistema cualquier salida puede calcularse en términos de la entrada y en una sucesión muy especial llamada respuesta a impulso queda caracterizado el sistema por completo. Esto puede verse de la siguiente manera: Tomando la identidad

y aplicando T en ambos lados

Por supuesto, esto tiene sentido sólo si

cae en el dominio de T. Pero como T es lineal e invariante en el entorno podemos escribir

Y como la salida y[k] está dada por

podemos escribir

Reemplazando

obtenemos finalmente

La sucesión es la respuesta a impulso del sistema representado por T. Como se observa arriba, es la salida del sistema cuando su entrada es un delta de Dirac discreto. Se obtienen resultados similares en sistemas de tiempo continuo.

Como ejemplo conceptual considere un globo dentro de un recinto, ubicado en un punto p. El globo explota y hace un sonido similar a un "pum". Aquí el recinto es un sistema T que toma el sonido "pum" y lo dispersa a través de múltiples reflexiones. La entrada δ_p[n] es el "pum", similar (debido en parte a su corta duración) a un delta de Dirac, y la salida es la sucesión del sonido afectado por el sistema, y depende de la ubicación (punto p) del globo. Si conocemos para cada punto del recinto conocemos la respuesta a impulso por completo del salón, y es posible predecir la respuesta del mismo a cualquier sonido producido en él.

Aplicaciones matemáticas

En lenguaje matemático, la respuesta a impulso de una transformación lineal es la imagen de la función Delta de Dirac sobre la transformación.

La transformada de Laplace de una respuesta a impulso es conocida como la función de transferencia. Usualmente es más fácil analizar sistemas usando funciones de transferencia en contraposición a las funciones de respuestas a impulso. La transformada de Laplace de la salida de un sistema puede determinarse mediante el producto entre la función de transferencia y la función entrada en el plano complejo, también conocido como el dominio espectral o de frecuencias. La transformada inversa de Laplace de éste resultado dará como resultado la función salida en el dominio temporal.

Para determinar la función de salida en el dominio temporal se requiere de la convolución de la función de entrada con la función de respuesta a impulso. Esto requiere el uso de integrales, y normalmente resulta más dificultoso que simplemente multiplicar dos funciones en el dominio espectral.

Aplicaciones prácticas

En los sistemas reales no es posible generar un impulso perfecto para aplicar como prueba en ninguna entrada. Por lo tanto, se usan aproximaciones de pulsos muy breves. Debido a que el pulso es suficiéntemente corto comparado a la respuesta a impulso, el resultado obtenido será bastante cercano a la respuesta a impulso teórica.