Delta de Dirac

Delta de Dirac
Diagrama esquemático de la función delta de Dirac.

La delta de Dirac (inapropiadamente llamada función delta de Dirac) es una distribución (función generalizada) introducida por primera vez por el físico inglés Paul Dirac y, como distribución, define un funcional en forma de integral sobre un cierto espacio de funciones. Se escribe como:

\delta_{a}(x) \equiv \delta(x-a)

Siendo \delta(x)\, para el caso a = 0\,

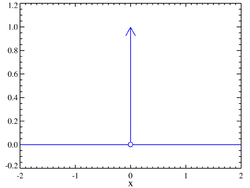
En física, la delta de Dirac puede representar la distribución de densidad de una masa unidad concentrada en un punto a. Esta función constituye una aproximación muy útil para funciones picudas y constituye el mismo tipo de abstracción matemática que una carga o masa puntual. En ocasiones se denomina también función de impulso. Además, la delta de Dirac permite definir la derivada generalizada de funciones discontinuas. Concretamente, se tiene la siguiente relación con la función escalón:

\delta_a(x) = \theta_a'(x)\,

Intuitivamente se puede imaginar la función δ(x) como una función que tiene un valor infinito en x = 0; tiene un valor nulo en cualquier otro punto, de tal manera que su integral es uno.

Contenido

Definiciones

La delta de Dirac es una función generalizada que viene definida por la siguiente fórmula integral:

\int_{-\infty}^\infty \delta(x-a) f(x) \, dx = f(a) \qquad \left[e.g. \int_{-\infty}^\infty \delta(x) \, dx = 1 \right ]

La delta de Dirac no es una función estrictamente hablando, puesto que se puede ver que requeriría tomar valores infinitos. A veces, informalmente, se define la delta de Dirac como el límite de una sucesión de funciones que tiende a cero en todo punto del espacio excepto en un punto para el cual divergería hacia infinito; de ahí la "definición convencional" dada por la también convencional fórmula aplicada a las funciones definidas a trozos:

\delta(x) = \begin{cases} \infty, & x = 0 \\ 0, & x \ne 0 \end{cases} ;

Es frecuente que en física la delta de Dirac se use como una distribución de probabilidad idealizada; técnicamente, de hecho, es una distribución (en el sentido de Schwartz).

En términos del análisis dimensional, esta definición de δ(x) implica que δ(x) posee dimensiones recíprocas a dx.

Definición como distribución de densidad

\int_a^b f(x) \delta (x-x_0) \,d x = \left\{\begin{matrix} f(x_0) & \mbox{si } a < x_0 < b \\ 0 & \mbox{si } x_0 < a \ \mbox{o} \ x_0 > b \end{matrix}\right.

Definición como límite de sucesiones de funciones

La delta de Dirac se define como "límite distribucional" de una sucesión de funciones que convergen puntualmente a la función cero en todos los puntos de su dominio excepto uno. Se dice que una sucesión de funciones fn(x) converge distribucionalmente cuando:

\left[ \lim_{n \to \infty} \int_{-\infty}^{\infty} f_n(x) \phi(x) dx \right] \to d(\phi)

Donde ϕ es una función perteneciente a un espacio vectorial de funciones, y d es un funcional continuo del espacio vectorial dual (el conjunto de esos elementos continuos es un subespacio vectorial del dual, conocido como espacio dual topológico del espacio original de funciones.

La delta de Dirac centrada se puede definir como el límite distribucional del funcional dado por d(ϕ) = ϕ(0), es decir, el límite en el sentido de las distribuciones de una sucesión de funciones tales que:

\left[ \lim_{n \to \infty} \int_{-\infty}^{\infty} f_n(x) \phi(x) dx \right] \to \phi(0)

Algunos ejemplos posibles de sucesión de funciones que cumpla lo anterior son:

\begin{matrix} f_n(x)=\begin{cases} n \quad \|x\|<\frac{1}{2n}\\ 0 \quad \|x\|\ge\frac{1}{2n} \end{cases} & f_n(x)=\cfrac{n}{\sqrt{\pi}}e^{-n^2x^2} \\ f_n(x)=\cfrac{1}{\pi}\cfrac{n}{n^2x^2+1} & f_n(x)=\cfrac{\sin nx}{\pi x} \end{matrix}

Propiedades

Estas propiedades se pueden demostrar multiplicando ambos miembros de cada igualdad por una función f(x) e integrando teniendo en cuenta que la función delta no puede formar parte del resultado a menos que esté dentro de una integral.

  • \delta(x)=\delta(-x)\,\!
  • f(x)\delta'(x)=-f'(x)\delta(x)\,\!
  • \delta'(x)=-\delta'(-x)\,\!
  • x^n\delta(x)=0 \qquad \forall n>0, x\in\mathbb{R}\,\!
  • (x-a)^n\delta(x-a)=0 \qquad \forall n>0\,\!
  • \delta(ax-b)=|a|^{-1}\delta(x-(b/a)) \qquad \forall a>0\,\!
  • h(x)\delta(x-a)=h(a)\delta(x-a)\,\!
  • h(x)\delta'(x-a) = h(a)\delta'(x-a)-h'(a)\delta(x-a)\,
  • \delta(f(x)) = \sum_n |f'(x_n)|^{-1}\delta(x-x_n), \quad \mbox{con}\ f(x_n)=0,\ f'(x_n)\ne 0
  • \delta(\omega) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} e^{-i\omega t}dt

En coordenadas esféricas se tiene:

\delta(\mathbf{r}-\mathbf{r}_0) = \begin{cases} \frac{1}{r^2\sin\theta}\delta(r-r_0) \delta(\theta-\theta_0)\delta(\phi-\phi_0) & x_0,y_0,z_0 \ne 0 \\ \frac{1}{2\pi r^2\sin\theta}\delta(r-r_0) \delta(\theta-\theta_0) & x_0=y_0=0,\ z_0 \ne 0 \\ \frac{1}{4\pi r^2}\delta(r-r_0) & x_0=y_0=z_0 = 0 \end{cases}

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Delta de Dirac — La función delta de Dirac fue introducida por primera vez por el físico inglés Paul Dirac y es una función que se representa de manera integral y que representa una distribución de densidad de una masa unidad concentrada en un punto a. Esta… …   Enciclopedia Universal

  • Delta de Dirac — Distribution de Dirac La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la… …   Wikipédia en Français

  • Fonction delta de Dirac — Distribution de Dirac La distribution de Dirac, aussi appelée par abus de langage fonction δ de Dirac, introduite par Paul Dirac, peut être informellement considérée comme une fonction δ qui prend une « valeur » infinie en 0, et la… …   Wikipédia en Français

  • Dirac-Stoß-Folge — Dirac Kamm Der Dirac Kamm (auch Dirac Stoß Folge oder Schah Funktion) beschreibt eine periodische Folge von Dirac Stößen. Anschaulich besitzt er die Form eines Kamms und wird wegen dieser Ähnlichkeit auch häufig mit dem kyrillischen Buchstaben Ш… …   Deutsch Wikipedia

  • Dirac Kamm — Der Dirac Kamm (auch Dirac Stoß Folge oder Schah Funktion) beschreibt eine periodische Folge von Dirac Stößen. Anschaulich besitzt er die Form eines Kamms und wird wegen dieser Ähnlichkeit auch häufig mit dem kyrillischen Buchstaben Ш (Schah)… …   Deutsch Wikipedia

  • Dirac delta function — delta funkcija statusas T sritis fizika atitikmenys: angl. delta function; Dirac delta function vok. Delta Funktion, f; Diracsche Delta Funktion, f rus. дельта функция, f; дельта функция Дирака, f pranc. fonction impulsion unité, f; fonction… …   Fizikos terminų žodynas

  • Dirac — bezeichnet: einen Roman von Dietmar Dath, siehe Dirac (Dath) einen Video Codec der BBC, siehe Dirac (Codec) Dirac ist der Name folgender Personen: Gabriel Andrew Dirac (1925–1984), britischer Mathematiker Paul Dirac (1902–1984), britischer… …   Deutsch Wikipedia

  • Dirac (desambiguación) — Saltar a navegación, búsqueda El término dirac puede referirse a: Dirac, códec. Paul Dirac, físico. Delta de Dirac, función matemática. Ecuación de Dirac, función física que describe al electrón. Mar de Dirac, modelo teórico del vacío, formulado… …   Wikipedia Español

  • Delta-Funktion — delta funkcija statusas T sritis fizika atitikmenys: angl. delta function; Dirac delta function vok. Delta Funktion, f; Diracsche Delta Funktion, f rus. дельта функция, f; дельта функция Дирака, f pranc. fonction impulsion unité, f; fonction… …   Fizikos terminų žodynas

  • delta function — delta funkcija statusas T sritis fizika atitikmenys: angl. delta function; Dirac delta function vok. Delta Funktion, f; Diracsche Delta Funktion, f rus. дельта функция, f; дельта функция Дирака, f pranc. fonction impulsion unité, f; fonction… …   Fizikos terminų žodynas

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”