Un arco continuo es un prisma mecánico cuyo eje baricéntrico es una curva plana y está sometido a cargas contenidas en el plano de curvatura o plano osculador del arco.

Un arco continuo es por tanto un elemento estructural curvo sometido predominante a esfuerzos axiles de compresión y flexión. Los arcos continuos estructuralmente diferentes de los tradicionales arcos de mapostería o fábrica que son elementos que trabajan a compresión sin flexión.

Contenido 1 Introducción 2 Descripción estructural 2.1 Ecuaciones de equilibrio 2.2 Tensiones 2.3 Desplazamientos 3 Véase también

Introducción

Los arcos continuos se construyen, generalmente de metal u hormigón armado, materiales que que pueden soportar también posibles tensiones de tracción debidas a la existencia de flexión en el arco. Aunque si el arco es suficientemente apuntado no existirán tensiones de tracción. En general un arco continuo estará sometido a un estado de flexión compuesta sin torsión, a diferencia de una viga balcón que estará sometida a flexión y torsión combiandas.

Los parámetros geométricos más importantes para dimensionar un arco continuo son además de la sección transversal, la longitud entre apoyos, y el apuntamiento que puede determinarse a partir de la longitud entre apoyos y el radio de curvatura.

Es interesante además notar que los arcos poco apuntados pueden sufrir un importante fenómeno de inestabilidad elástica que se circunscribe sólo a arcos y cúpulas, conocido por su nombre inglés como snap-through.

Descripción estructural

Una restricción importante en los arcos en que predomina la flexión, es que estos deben ser continuos, de ahí el nombre de arco continuos, y no formados por bloques, tal como sucede en los arcos de mampostería.

Ecuaciones de equilibrio

Las ecuaciones de equilibrio que relacionan los esfuerzos internos de los arcos continuos con las fuerzas exteriores aplicadas son:

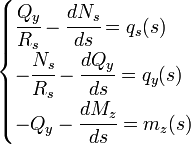
Donde:

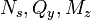, son los esfuerzos internos: esfuerzo axil a lo largo de la directriz curva, esfuerzo cortante perpendicular a la directriz y momento flector.

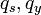, son las fuerzas paralela y perpendicular a la directriz por unidad de longitud y m_z el flector por unidad de longitud.

es la longitud de arco a lo largo de la directriz del arco.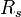

es el radio de curvatura en cada punto de la directriz del arco.

Como se puede ver en la tercera de estas ecuaciones en un arco continuo a diferencia de lo que sucede con un arco clásico de mampostería existen momentos flectores.

Tensiones

Los esfuerzos internos de un arco continuo se relacionan con las tensiones seccionales mediante las siguientes ecuaciones:

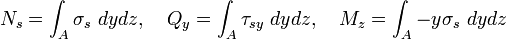
Para calcular las tensiones en función de esfuerzos conocidos se puede aplicar la propia teoría de Navier-Bernouilli para vigas.

Desplazamientos

Los desplazamientos horizontal u y vertical v, así como el giro θ pueden obtenerse a partir de los esfuerzos internos resolviendo el siguiente sistema de primer orden:

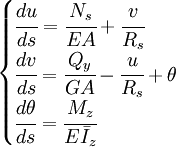
Donde:

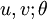son respectivamente los desplazamientos y el giro.

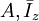son el área transversal y el momento de inercia corregido.

Véase también

• Viga balcón