- Aritmética Modular Compleja
-
Aritmética Modular Compleja
La ‘Aritmética Modular Compleja’ (hacia un nuevo test de primalidad)
La ‘Aritmética Modular Compleja’.La ‘semiarcotangente discreta’
La ecuación diofántica
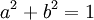 no tiene sentido en la aritmética normal, ya que se reduce a las solución trivial que bien a
no tiene sentido en la aritmética normal, ya que se reduce a las solución trivial que bien a 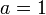 ó
ó 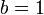 pero lo tiene si la llevamos al mundo de la aritmética modular:
pero lo tiene si la llevamos al mundo de la aritmética modular: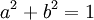 (mod M)
(mod M)Por que podemos encontrar muchas soluciones no triviales que la cumplen. Para ello lo más práctico es usar las relaciones entre la
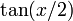 y el
y el 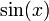 y el
y el 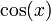 :
: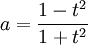
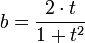
Obviamente, una vez visto este paralelismo, esto nos lleva al establecimiento de otro mucho más amplio con la variable compleja, es decir que son factibles las operaciones:
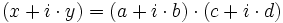 (mod M) siendo
(mod M) siendo 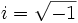
resultado:
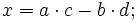 (mod M)
(mod M)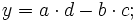 (mod M)
(mod M)siendo el caso de
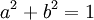 (mod M) un subconjunto de otro más general. Esto conviene señalarlo para cuando sea necesario implementar los algoritmos de cálculo, para evitar las operaciones para encontrar el inverso modular (algoritmo extendido de Euclides)de
(mod M) un subconjunto de otro más general. Esto conviene señalarlo para cuando sea necesario implementar los algoritmos de cálculo, para evitar las operaciones para encontrar el inverso modular (algoritmo extendido de Euclides)de 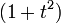 más veces que las estrictamente necesarias.
más veces que las estrictamente necesarias.O sea que, en el fondo, es lo mismo que las conocidas fórmulas de
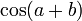 y
y 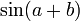 .
.Como es natural es posible calcular el
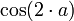 y el
y el 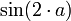 y siguiendo un método similar al que se usa para la implementación de la exponencial modular simple (RSA) calcular en tiempo polinomial el equivalente al
y siguiendo un método similar al que se usa para la implementación de la exponencial modular simple (RSA) calcular en tiempo polinomial el equivalente al 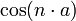 y el
y el 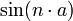 , lo que en el fondo no deja de ser similar al
, lo que en el fondo no deja de ser similar al 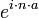 ,pero usando aritmética modular. La manera más simple es la descomposición del exponente 'n' en la suma de las sucesivas potencias de dos.
,pero usando aritmética modular. La manera más simple es la descomposición del exponente 'n' en la suma de las sucesivas potencias de dos.Una vez obtenidos el
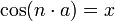 y el
y el 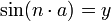 podemos obtener el valor de
podemos obtener el valor de 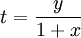 correspondiente, que da origen, salvo singularidades a estos
correspondiente, que da origen, salvo singularidades a estos 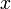 e
e 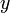 , tales que
, tales que 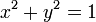 (mod M).
(mod M).A estos valores de
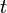 podría llamarse la `semiarcotangente discreta´ por el paralelismo con la ecuación
podría llamarse la `semiarcotangente discreta´ por el paralelismo con la ecuación 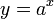 (mod M) (exponencial modular simple) donde se le llama `logaritmo discreto´.
(mod M) (exponencial modular simple) donde se le llama `logaritmo discreto´.El `Indicador imaginario de Euler´: IiE (M)
En el caso de la exponencial modular simple
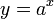 (mod M), como ya es conocido existe el `Indicador de Euler´ (IE (M)) (función φ de Euler) que no es otra cosa que un número tal que
(mod M), como ya es conocido existe el `Indicador de Euler´ (IE (M)) (función φ de Euler) que no es otra cosa que un número tal que 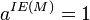 (mod M), para todo
(mod M), para todo 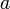 . Pues bien, aquí también ocurre lo mismo, es decir que al calcular el
. Pues bien, aquí también ocurre lo mismo, es decir que al calcular el 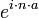 , existe un valor de
, existe un valor de 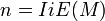 que nos lleva al
que nos lleva al 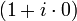 ,
, 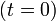 el neutro de la variable compleja, y que tiene características similares con el `indicador de Euler´ , pero no iguales.
el neutro de la variable compleja, y que tiene características similares con el `indicador de Euler´ , pero no iguales.Vamos por partes, empecemos estudiando el problema para el caso de que
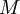 sea un número primo. A excepción del 2 todos los números primos son impares y podemos clasificarlos en dos tipos, unos que son de la forma
sea un número primo. A excepción del 2 todos los números primos son impares y podemos clasificarlos en dos tipos, unos que son de la forma 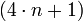 y otros que son de la forma
y otros que son de la forma 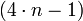 . Empíricamente se ha visto que el
. Empíricamente se ha visto que el 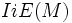 era en ambos casos
era en ambos casos 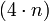 , es decir ,el múltiplo de cuatro más próximo, por exceso o por defecto, a
, es decir ,el múltiplo de cuatro más próximo, por exceso o por defecto, a 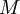 , por ejemplo:
, por ejemplo: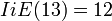
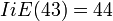
¿Por qué es esto así?. En el apartado anterior se ha visto que dada una `semiarcotangente discreta´
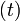 , podemos encontrar un
, podemos encontrar un 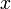 e
e 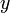 tales que
tales que 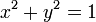 (mod M).
(mod M).Los valores posibles de
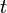 , estarán obviamente comprendidos entre el cero y el
, estarán obviamente comprendidos entre el cero y el 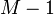 , pero además, salvo excepciones, se agrupan de cuatro en cuatro según que el resultado de
, pero además, salvo excepciones, se agrupan de cuatro en cuatro según que el resultado de 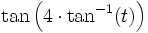 (mod M), sea el mismo valor. Estos valores son:
(mod M), sea el mismo valor. Estos valores son: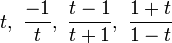
Lo que se deduce fácilmente `sumando´ o `restando´
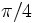 en el paralelismo de las funciones trigonométricas.
en el paralelismo de las funciones trigonométricas.Esto es claramente salvo las `excepciones´, que ahí es donde está la clave del asunto: Una `excepción´, que existe siempre, es la que podemos asociar al `neutro´ ya que solo podemos agrupar tres valores:
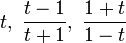 ya que el otro
ya que el otro 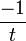 no tiene sentido para
no tiene sentido para 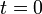 .
.La otra `excepción´ solo ocurre para los primos del tipo
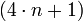 en la que existe un grupo de dos soluciones singulares de
en la que existe un grupo de dos soluciones singulares de 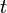 , tales que
, tales que 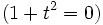 (mod M). Esto ya lo sabían Fermat y sus amigos, ya que es consecuencia de que cuando un número primo es de esta forma puede descomponerse en una suma de cuadrados.
(mod M). Esto ya lo sabían Fermat y sus amigos, ya que es consecuencia de que cuando un número primo es de esta forma puede descomponerse en una suma de cuadrados.Siguiendo con el paralelismo del `indicador de Euler´ en el caso de potencias de un número primo el comportamiento es similar:
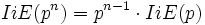 .
.Pero en el caso del producto de varios primos o de sus potencias, el
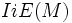 es el mínimo común múltiplo de los factores (estamos `girando'
es el mínimo común múltiplo de los factores (estamos `girando' 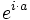 ).
).El nuevo `test de primalidad´
Parecido al de Euler, mejor dicho de Fermat:
Es condición necesaria, que :
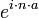 (mod M)
(mod M) 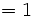 (variable compleja) y para todo
(variable compleja) y para todo 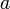 siendo
siendo 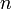 el múltiplo de cuatro ,más próximo a
el múltiplo de cuatro ,más próximo a 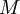 , para que
, para que 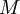 sea primo
sea primoLos `nuevos números de Carmichael´
En el test de primalidad de Fermat existían los números de Carmichael, que cumplían la condición de primalidad, sin ser primos, como por ejemplo el 561. La propiedad que deben cumplir estos números es que el
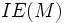 tenga muchos divisores comunes con
tenga muchos divisores comunes con 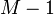 , veamos con el ejemplo:
, veamos con el ejemplo: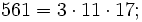
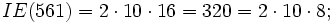
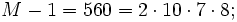
En el caso de la aritmética modular compleja, pasa algo parecido, tendremos un `pseudoprimo' cuando el
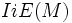 sea divisor de
sea divisor de 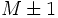 , por ejemplo:
, por ejemplo:El
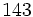 ,
, 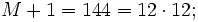 El
El 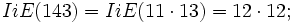
Luego
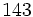 será un `pseudoprimo´, Pero ...
será un `pseudoprimo´, Pero ...La aplicación a la vez de ambos criterios, es una buena forma de eliminar `pseudoprimos´. Lamentablemente no es suficiente ya que existirán números de Carmichael que cumplan ambos criterios, el más pequeño encontrado es el 6601:
En efecto
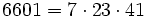 , es un número de Carmichael, y su
, es un número de Carmichael, y su 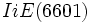 es
es 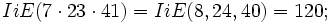 6600 es múltiplo exacto de 120.
6600 es múltiplo exacto de 120.`El `nuevo test de Miller-Rabin´
Si podemos encontrar un número
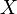 tal que
tal que 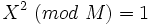 , siendo
, siendo 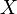 distinto de
distinto de 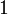 o de
o de 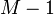 , es evidente que
, es evidente que 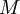 no es un número primo. Esto es precisamente lo que da origen a grandes rasgos al test de primalidad de Miller-Rabin clásico, ya que en un pseudoprimo se cumple la condición:
no es un número primo. Esto es precisamente lo que da origen a grandes rasgos al test de primalidad de Miller-Rabin clásico, ya que en un pseudoprimo se cumple la condición: 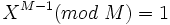
Como
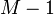 es par al ir dividiendo el exponente
es par al ir dividiendo el exponente 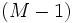 por dos, sucesivamente hasta que quede impar, es posible llegar a conseguir una solución no trivial de un residuo cuadrático igual a la unidad, y deducir que
por dos, sucesivamente hasta que quede impar, es posible llegar a conseguir una solución no trivial de un residuo cuadrático igual a la unidad, y deducir que 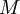 no es primo.
no es primo.De similar manera al
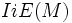 se le puede ir dividiendo sucesivamente por dos, y llegar a la mismas deducciones. Obviamente este tipo de test son el `talón de Aquiles´ de los números de Carmaichael.
se le puede ir dividiendo sucesivamente por dos, y llegar a la mismas deducciones. Obviamente este tipo de test son el `talón de Aquiles´ de los números de Carmaichael.Introducción a las posibles demostraciones asociadas
Sean
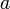 y
y 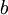 dos números tales que
dos números tales que 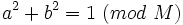 podemos decir simbólicamente que:
podemos decir simbólicamente que: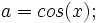
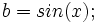
por lo que si desarrollamos por la fórmula del Binomio de Newton:
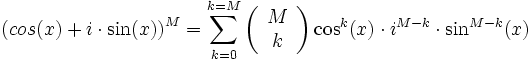
ahora bien, si
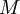 es primo:
es primo: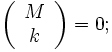 (mod M) para todo
(mod M) para todo 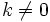 ó
ó 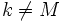
entonces:
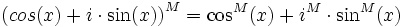
pero si
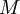 es primo, por el Pequeño teorema de Fermat:
es primo, por el Pequeño teorema de Fermat: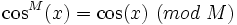 y
y 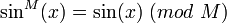 o sea:
o sea: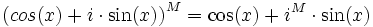
entonces como:
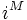 será igual a
será igual a 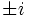 según
según 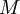 (mod 4) sea
(mod 4) sea 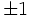 , bastará pues con multiplicar por:
, bastará pues con multiplicar por: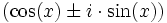 para obtener el
para obtener el 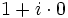
con lo que resumiendo si:
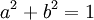 (mod M) siendo
(mod M) siendo 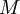 primo se cumplirá que:
primo se cumplirá que: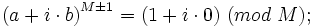 según
según 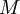 (mod 4) sea
(mod 4) sea 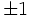
Fuentes en lenguaje C
/***************************************************************** Este programa calcula todos números primos menores a 10000 sin dar ningun falso primo por comparación de los resultados de (1+a)^n, (1-a)^n ,(1+ia)^n e (1-ia)^n (mod m) para a=5 aunque descarta antes los multiplos de 5 ************************************/ #include <stdio.h> #include <math.h> unsigned long suma_mod(unsigned long x,unsigned long y,unsigned long m){ unsigned long z; __int64 l; l=(unsigned long)x; l+=y; l%=m; z=(unsigned long) l; return(z);} unsigned long resta_mod(unsigned long x,unsigned long y,unsigned long m){ unsigned long z; __int64 l; l=(unsigned long) m; l+=x; l-=y; l%=m; z=(unsigned long) l; return(z);} unsigned long mult_mod(unsigned long x,unsigned long y,unsigned long m){ unsigned long z; __int64 l; l=(unsigned long)x; l*=y; l%=m; z=(unsigned long) l; return(z);} unsigned long eleva_mod(unsigned long x,unsigned long e,unsigned long m){ unsigned long z,ei,p; short i; ei=e; z=1; p=x; for(i=0;i<32;i++){ if((ei&0x1l)==1) z=mult_mod(z,p,m); p=mult_mod(p,p,m); ei>>=1; } return(z);} char Euclides(unsigned long *y,unsigned long x,unsigned long mod){ char s=1,ok=0; unsigned long n,d,ia,ib,ix,c,r=0; if(x!=0){ ok=1; n=mod; d=x; ia=0; ib=1; } while(ok){ c=n/d; r=n-c*d; ix=ib*c+ia; if((r==0)||(r==1)) break; n=d; d=r; ia=ib; ib=ix; s^=0x01; } if(r==0){ ok=0; *y=d; } if(r==1){ ok=1; if(s) *y=mod-ix; else *y=ix; } return(ok);} char x2_y2_1(unsigned long t,unsigned long *c,unsigned long *s,unsigned long mod){ char ok,okfac; unsigned long xx,yy,aa,cc,fac=1,facx1,facx2; cc=mult_mod(t,t,mod); yy=suma_mod(t,t,mod); xx=resta_mod(1,cc,mod); cc=suma_mod(1,cc,mod); okfac=Euclides(&facx1,xx,cc); if(okfac==0) okfac=Euclides(&facx2,yy,cc); if(okfac==0) okfac=Euclides(&fac,facx1,facx2); if((okfac!=0)||(fac==0)) fac=1; xx/=fac; yy/=fac; cc/=fac; if(cc==1){ ok=1; aa=1; } else ok=Euclides(&aa,cc,mod); if(ok){ *c=mult_mod(xx,aa,mod); *s=mult_mod(yy,aa,mod); } return(ok);} void sc_amasb(unsigned long mod,unsigned long ca,unsigned long sa, unsigned long cb,unsigned long sb, unsigned long *cx,unsigned long *sx){ unsigned long x,y; x=mult_mod(sa,cb,mod); y=mult_mod(sb,ca,mod); *sx=suma_mod(x,y,mod); x=mult_mod(ca,cb,mod); y=mult_mod(sa,sb,mod); *cx=resta_mod(x,y,mod); } char sc_n_x(unsigned long mod,unsigned long n,unsigned long t, unsigned long *cx,unsigned long *sx){ char ok; unsigned long i,c,s,ci,si,c2,s2; ok=x2_y2_1(t,&ci,&si,mod); c=1;s=0; if(ok){ i=n; while(i!=0){ if((i&1)==1) sc_amasb(mod,c,s,ci,si,&c,&s); sc_amasb(mod,ci,si,ci,si,&c2,&s2); ci=c2;si=s2; i>>=1; } *cx=c;*sx=s; } return (ok);} void sc0_n_x(unsigned long mod,unsigned long n, unsigned long c0,unsigned long s0, unsigned long *cx,unsigned long *sx){ unsigned long i,c,s,ci,si,c2,s2; ci=c0; si=s0; c=1; s=0; i=n; while(i!=0){ if((i&1)==1) sc_amasb(mod,c,s,ci,si,&c,&s); sc_amasb(mod,ci,si,ci,si,&c2,&s2); ci=c2;si=s2; i>>=1; } *cx=c;*sx=s; } char unsigned long t_cs(unsigned long *t,unsigned long c,unsigned long s,unsigned long m){ unsigned long sf,c1,cf,ic1,f,fac=1; char ok,okfac; c1=suma_mod(1,c,m); okfac=Euclides(&f,s,c1); if((okfac==0)&&(f!=0)) fac=f; cf=c1/fac; sf=s/fac; if(cf==1){ ok=1; ic1=1; } else ok=Euclides(&ic1,cf,m); if(ok) *t=mult_mod(sf,ic1,m); return(ok);} char coef_iie(unsigned long *c1,unsigned long *c2,unsigned long *c3,unsigned long *c4,unsigned long a,unsigned long m){ unsigned long ia,i2,x1,x2,a1,a2,a3,a4,b1,b2,b3,b4; char ok; ok=Euclides(&i2,2,m); if(ok){ ok=0; if(a>=2) ok=Euclides(&ia,a,m); if(a==1) { ok=1; ia=1; } } if(ok){ x1=suma_mod(1,a,m); x2=resta_mod(1,a,m); x1=eleva_mod(x1,m,m); x2=eleva_mod(x2,m,m); a1=suma_mod(x1,x2,m); a2=resta_mod(x1,x2,m); a1=mult_mod(a1,i2,m); a2=mult_mod(a2,i2,m); x1=1; x2=a; sc0_n_x(m,m,x1,x2,&a3,&a4); if((m%4)==3) a4=m-a4; x1=suma_mod(a1,a3,m); x2=resta_mod(a1,a3,m); b1=mult_mod(x1,i2,m); b2=mult_mod(x2,i2,m); x1=suma_mod(a2,a4,m); x2=resta_mod(a2,a4,m); b3=mult_mod(x1,i2,m); b4=mult_mod(x2,i2,m); *c1=b1; *c2=b2; b3=mult_mod(b3,ia,m); *c3=b3; *c4=b4; } return(ok);} char ok_primo(unsigned long m){ char ok=1; unsigned long a,c1,c2,c3,c4; a=5; if(ok) ok=coef_iie(&c1,&c2,&c3,&c4,a,m); if(ok) { if((c1!=1)||(c2!=0)||(c3!=1)||(c4!=0)) ok=0;} if(m==2) ok=1; if(m==3) ok=1; if(m==5) ok=1; return(ok);} main(){ unsigned long i,n=0,k=10000; char ok; for(i=2;i<k;i++){ ok=ok_primo(i); if(ok){ printf("%d,",i); n++; } } printf("\nk=%d,n=%d\n",k,n); return(0);}
Referencia
- ANÁLISIS ALGEBRÁICO POR A.FZ.DE TROCONIZ Y E.BELDA VILLENA. ED. VIZCAINA 1964 (BILBAO) Cap. II y VII
Categoría: Aritmética modular
Wikimedia foundation. 2010.
