Superficie de fluencia

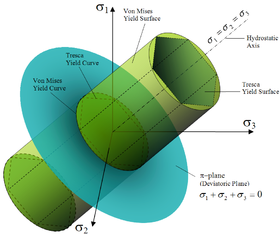Comparación de las superficies de fluencia para los criterios de Von Mises y Tresca en usando las tensiones principales como coordenadas.

La superficie de fluencia de un material es una construcción abstracta que permite visualizar el conjunto de tensiones posibles o admisibles dentro de un sólido deformable elastoplástico.

Introducción

El estado tensional de un sólido deformable puede caracterizarse mediante tres valores de tensión según tres direcciones perpendiculares conocidas como tensiones principales de tensión, siendo los tres valores de tensión las llamadas tensiones principales. Por eso así el estado tensional en ese punto puede representarse por un espacio tridimensional . La superficie de fluencia es una superficie bidimensional en dicho espacio de tensiones.

Cuando un sólido deformable se somete a tensiones progresivamente mayores, la energía potencial elástica se incrementa y a partir de cierto punto se producen transformaciones termodinámicas irreversibles al superar dicha energía cierto valor. El conjunto de puntos por debajo de los cuales no se producen transformaciones termodinámicas irreversibles es el conjunto de tensiones admisibles es una región conexa del espacio de tensiones. La frontera de la región de tensiones admisibles es precisamente superficie de fluencia.

Plasticidad perfecta

Un material elastoplástico se dice que presenta plasticidad perfecta, si sea cual sea el valor de las tensiones en un punto, la superficie de fluencia no cambia ni de forma ni de posición en el espacio abstracto de tensiones. Cuando un material presenta plasticidad perfecta las ecuaciones constitutivas no necesitan incluir variables internas ni esfuerzos conjugados asociados y el problema elastoplástico es más sencillo.

Los materiales reales sin embargo casi siempre presentan plasticidad imperfecta, y la superficie de fluencia puede sufrir desplazamientos, tal como sucede en el efecto Bauschinger. Los cambios de forma, generalmente están asociados al comportamiento de endurecimiento, aumentando en ese caso el volumen encerrado en la superficie de fluencia.

Propiedades de la superficie de fluencia

• Convexidad. Bajo argumentos termodinámicos puede probarse que, La superficie de fluencia es convexa.^[1]
• Compacidad. La superficie de fluencia se considera cerrada y por tanto encierra un volumen finito. Y por tanto el conjunto de tensiones alcanzables es siempre un conjunto compacto.
• Continuidad. La superfiecie de fluencia se considera que es Lipshitz-continua.
• Unicidad del problema elastoplástico. Cuando la superficie no es diferenciable el problema elastoplástico puede ser tratado mediante métodos variacionales. Bajo condiciones suficientemente regulares puede probarse que la solución del problema elastoplástico, aun cuando la superficie no sea diferenciable, es única.^[2]

Referencia

Bibliografía

• Weimin Han & B. Daya Reddy: Plasticity: Mathematical Theory and Numerical Analysis, Springer-Verlag, Nueva York, 1999, ISBN 0-387-98704-5.

Ejemplos