- Teorema de la aproximación lineal
-
Teorema de la aproximación lineal
Se debe suponer que z=f (x, y) es una función que posee derivadas parciales continuas en un punto (a, b). Por lo tanto el incremento ∆z en el punto (a, b) está dado por:
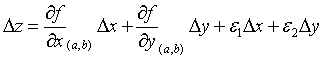
Demostración
Por definición:
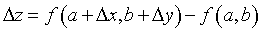
Luego, se suma y resta el siguiente término:
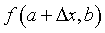
Entonces nos queda:
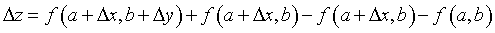
Separando convenientemente:
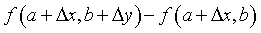 (1)
(1)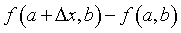 (2)
(2)Se puede aplicar a (1) el teorema del valor medio de Lagrange, f (b) – f (a) = f’(c) (b –a), donde c es un número arbitrario, interior al intervalo (a, b):
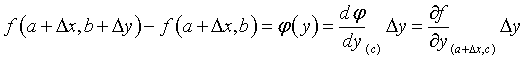
Como c es interior a (b, b+∆y):
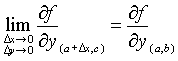
Sabiendo que f (x) = L+ε, entonces:
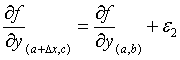
Por lo tanto, (1) queda:
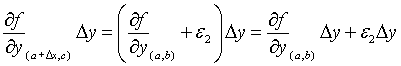
Se puede aplicar el mismo razonamiento para (2),
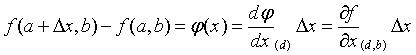
El número arbitrario d es interior a (a, a+∆x):
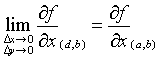
Entonces queda,
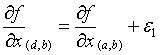
Y (2) resulta:
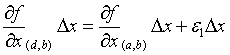
Como ∆z = (1) + (2), entonces:
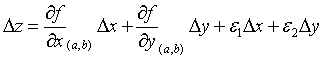 Categoría: Análisis matemático
Categoría: Análisis matemático
Wikimedia foundation. 2010.
