Teorema de la bisectriz

Teorema de la bisectriz
En este diagrama, siendo A el ángulo bisecado, BA:AC = BD:DC

El teorema de la bisectriz del ángulo interno de un triángulo es un teorema de la geometría elemental la cual es una consecuencia o corolario del Teorema de Tales.

En un triángulo, la razón entre dos lados es igual a la razón de las partes en las que queda dividido el tercer lado por la bisectriz de ángulo interno opuesto.

O lo que es equivalente:

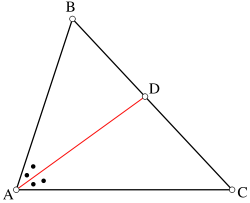
Dado el triángulo ABC, sea AD la bisectriz del ángulo interno A, entonces se cumple la proporción: \frac {BA}{AC} = \frac {BD}{DC}

Contenido

Demostración 1

Figura bz1 Demostración del teorema de la bisectriz aplicando la «Ley de senos».

Nomenclatura (correspondiente a la Figura bz1):

|AC| \equiv b \; ,
|BC| \equiv a \; ,
|AD| \equiv m \; ,
|BD| \equiv n \; ,
\angle ACD \equiv \angle DCB \equiv x \; ,
\angle ADC \equiv y \; .

Aplicando el teorema del seno al triángulo \scriptstyle \Delta ADC tenemos:

(bz01) {m \over \sin x} = {b \over \sin y}

Los ángulos “y” y “π-y” son suplementarios, lo cual implica que \scriptstyle \sin (\pi -y) = \sin (y), entonces aplicando ahora el teorema del seno al triángulo \scriptstyle \Delta DBC tenemos:

(bz02) {n \over \sin x} = {a \over \sin y}

Dividiendo m.a.m. la ecuación (bz01) por la ecuación (bz02) y simplificando obtenemos: {m \over n} = {b \over a}, ∎.[1]

Demostración 2

Dibujando desde C una línea paralela a la recta AD hasta encontrar la prolongación de lado BA a partir del lado A y encontrándose en el punto E. El triángulo ACE es isósceles porque sus ángulos C y E son congruentes:

A\widehat CE = C\widehat AD

porque los dos ángulos son alternos internos respecto a las rectas paralelas AD y EC cortadas por la recta transversal AC

A\widehat EC = B\widehat AD

porque son correspondientes a las rectas paralelas AD y EC a las cuales corta la recta BE, además

C\widehat AD = B\widehat AD

porque los ángulos creados por la bisectriz son iguales.

Por la propiedad transitiva de la igualdad se tiene que

A\widehat EC = A\widehat CE

Por tanto los segmentos AC y AE son congruentes. Por el Teorema de Thales se mantiene la proporción:

\frac {BA}{AE} = \frac {BD}{DC}

y ya que AC y AE son congruentes, también se cumple que

\frac {BA}{AC} = \frac {BD}{DC}

Demostración 3

El triángulo \triangle ABD y el triángulo \triangle ACD comparten altura h, y si (ABD) y (ACD) representan sus respectivas áreas, se cumple que:

\frac {(ABD)}{(ACD)} = \frac {BD \cdot h}{CD \cdot h} = \frac {BD}{CD}

Sean F y G los pies de altura de los triángulos ABD y ACD en AB y AC respectivamente. EL ángulo BAD es congruente con el ángulo CAD, por ser AD bisectriz.

Los ángulos AFD y AGD son iguales a π/2 rad (90°) y congruentes entre sí, por ser los pies de las alturas.

Por lo tanto, los ángulos ADF y ADG son congruentes. Entonces el triángulo \triangle ADF y el triángulo \triangle ADG son congruentes, por el criterio ángulo–lago–ángulo (ALA), pues además comparten el lado AD.

Con lo que se obtiene que:

DF = DG

Pero DF y DG son las alturas de los triángulos \triangle ABD y \triangle ACD respectivamente. Por lo tanto la razón entre sus áreas es igual a la razón entre sus bases:

\frac {(ABD)}{(ACD)} = \frac {AB \cdot h}{AC \cdot h} = \frac {AB}{AC}

Por transitividad con lo establecido anteriormente, se tiene que:

\frac {AB}{AC} = \frac {BD}{CD}

Demostración 4

Sean los ángulos:

B\widehat AD = C\widehat AD = \alpha
A\widehat DB = \theta

Entonces:

A\widehat DC = 180- \theta

Considerando el triángulo ABD, por el Teorema del seno se obtiene que: \frac {BD}{sen(\alpha)} = \frac {AB}{sen(\theta)}

Considerando el triángulo ACD se obtiene que: \frac {CD}{sen(\alpha)} = \frac {AC}{sen(180- \theta)}

Pero se conoce la siguiente identidad: \operatorname{sen}(x) = \operatorname{sen}(180-x)

Entonces la ecuación queda: \frac {CD}{sen(\alpha)} = \frac {AC}{sen(\theta)}

Dividiendo las dos igualdades se obtiene: \frac {BD \cdot sen(\alpha)}{CD \cdot sen(\alpha)} = \frac {AB \cdot sen(\theta)}{AC \cdot sen(\theta)}

Simplificando: \frac {AB}{AC} = \frac {BD}{CD}

Notas y referencias

  1. ↑ Unicode indica que el cuadrado relleno (∎), como símbolo matemático, significa ‘fin de la prueba’ (en inglés ‘end of proof’) o también QED (Quod erat demonstrandum).

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Bisectriz — Saltar a navegación, búsqueda La bisectriz es la recta que divide al ángulo en dos partes iguales. Contenido 1 Propiedad 2 Aplicación 3 Otras propiedades 4 …   Wikipedia Español

  • Circunferencia de Apolonio — La circunferencia de Apolonio, se trata de un famoso problema de lugares geométricos: Figura 1: definición de un círculo por Apolonio …   Wikipedia Español

  • Triángulo — Para otros usos de este término, véase Triángulo (desambiguación). El triángulo es un polígono de tres lados. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran… …   Wikipedia Español

  • Ceviana — Triángulo con una ceviana d. Ceviana es un segmento de recta que une un vértice de un triángulo con el lado opuesto a este. También se la conoce como transversal angular. Se puede decir que la mediana, la altura o la bisectriz son cevianas o… …   Wikipedia Español

  • Proyección isométrica — Una proyección isométrica es un método gráfico de representación, más específicamente una axonométrica[1] cilíndrica[2] ortogonal.[3] Constituye una representación visual de un objeto tridimensional en dos dimensiones, en la que los tres ejes… …   Wikipedia Español

  • Punto medio — Saltar a navegación, búsqueda Punto medio de un segmento, hallado mediante regla y compás. Para otros usos de este término, véase punto medio (filosofía). Para para la falacia argumentativa, véase falacia del punto medio …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”