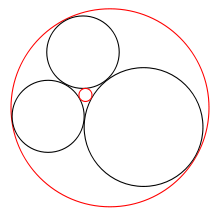
- Teorema de los círculos de Descartes
-
En geometría, el teorema de los círculos de Descartes establece la relación entre cuatro círculos tangentes entre sí por medio de su curvatura.
Contenido
Historia
Este problema geométrico ha sido abordado por milenios. En la grecia antigua, del siglo III a. C. Apolonio de Perga dedicó un libro entero al tema, lamentablemente el libro llamado Sobre tangencias, no está entre sus obras sobrevivientes.
René Descartes abordó el problema en 1643, en una carta a la princesa Isabel I de Bohemia. Da una solución al problema, y por lo tanto, se atribuye su nombre al teorema.
Frederick Soddy redescubrió en 1936 la solución, por lo cual, este problema es a veces conocido como los círculos besadores de Soddy , porque Soddy escogió para publicar su versión del teorema en la forma de un poema titulado The Kiss Precise, publicado en la revista Nature (20 de junio de 1936). Soddy también extendió el teorema de las esferas; Thorold Gosset prorrogó el teorema a dimensiones arbitrarias.
Definición de curvatura
Círculos tangentes. Dado tres círculos mutuamente tangentes (negro), ¿Cuál es el radio del cuarto círculo? . En general hay dos soluciones posibles (rojo).
El teorema es más fácil de enunciar en términos de la curvatura de los círculos. La curvatura de un círculo se define como k = 1 / r, donde r es el radio. Mientras más grande el círculo, menor es la magnitud de su curvatura, y viceversa.
Si consideramos una línea recta como un círculo degenerado de curvatura k = 0, el teorema es igualmente aplicable.
Teorema
Si cuatro círculos son mutuamente tangentes de curvatura ki (para cada i = 1,...,4), el teorema nos dice:
UNIQ66a02221174e6b6d-math-00000006-QINU Al tratar de encontrar el radio del cuarto círculo tangente a los otros tres círculos, la ecuación se reescribe como:
UNIQ66a02221174e6b6d-math-00000008-QINU - k4 = k1 + k2 + k3 + sqrtk1k2 + k2k3 + k3k1.
Véase también
Categorías:- Teoremas de geometría
- René Descartes
- Geometría euclidiana plana
- Círculos
Wikimedia foundation. 2010.
