Teorema

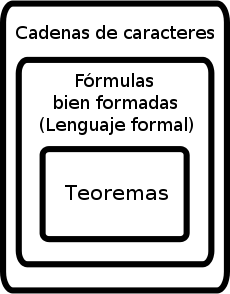Esta imagen muestra la relación entre las cadenas de caracteres, las fórmulas bien formadas y los teoremas. En algunos sistemas formales, sin embargo, el conjunto de los teoremas coincide con el de las fórmulas bien formadas.

Un teorema es una afirmación que puede ser demostrada dentro de un sistema formal. Demostrar teoremas es un asunto central en la matemática.

Un teorema generalmente posee un número de premisas que deben ser enumeradas o aclaradas de antemano. Luego existe una conclusión, una afirmación matemática, la cual es verdadera bajo las condiciones dadas. El contenido informativo del teorema es la relación que existe entre la hipótesis y la tesis o conclusión.

Se llamará corolario a una afirmación lógica que sea consecuencia inmediata de un teorema, pudiendo ser demostrada usando las propiedades del teorema previamente demostrado.

Terminología

En matemática una afirmación debe ser interesante o importante dentro de la comunidad matemática para ser considerada un teorema. Las afirmaciones menos importantes se denominan:

• Lema: una afirmación que forma parte de un teorema más amplio. El lema de Gauss y el lema de Zorn, por ejemplo, son considerados demasiado importantes per se para algunos autores, por lo cual consideran que la denominación lema no es adecuada.
• Corolario: una afirmación que sigue inmediatamente a un teorema. Una proposición A es un corolario de una proposición o teorema B si A puede ser deducida sencillamente de B.
• Proposición: una afirmación o resultado no asociado a ningún teorema en particular.

Una afirmación matemática que se cree verdadera pero no ha sido demostrada se denomina conjetura o hipótesis. Por ejemplo: la conjetura de Goldbach o la hipótesis de Riemann.

Teoremas dentro de la lógica matemática

Un teorema requiere de un marco lógico; este marco consistirá en un conjunto de axiomas (sistema axiomático) y un proceso de inferencia, el cual permite derivar teoremas a partir de los axiomas y teoremas que han sido derivados previamente.

En lógica matemática y lógica proposicional, cualquier afirmación demostrada se denomina teorema. Más concretamente en lógica matemática se llama demostración a una secuencia finita de fórmulas bien formadas (fórmulas lógicas bien formadas) F₁, ...,F_n, tales que cada F_i es o bien un axioma o bien un teorema que se sigue de dos fórmulas anteriores F_j y F_k (tales que j<i y k<i) mediante una regla de deducción. Dada una demostración como la anterior si el elemento final F_n no es un axioma entonces es un teorema.

Resumiendo lo anterior puede decirse formalmente, un teorema es una fórmula bien formada, que no es un axioma, y que puede ser el elemento final de alguna demostración, es decir, un teorema es una fórmula lógica bien formada para la cual existe una demostración.

Teoremas dentro de otras ciencias

Con frecuencia en física o economía algunas afirmaciones importantes que pueden ser deducidas o justificadas a partir de otras afirmaciones o hipótesis básicas se llaman comúnmente teoremas. Sin embargo, frecuentemente las áreas de conocimiento donde aparecen esas afirmaciones con frecuencia no han sido formalizadas adecuadamente en forma de sistema axiomático por lo que estrictamente debería usarse con cautela el término teorema para referirse a esas afirmaciones demostrables o deducibles de supuestos "más básicos".

Véase también

• Teorema de incompletitud de Gödel
• Sistema axiomático