Teorema fundamental sobre homomorfismos
- Teorema fundamental sobre homomorfismos
-
Teorema fundamental sobre homomorfismos
En álgebra abstracta, para un número de estructuras algebraicas, el teorema fundamental sobre homomorfismos relaciona la estructura de dos objetos entre los cuales se dé un homomorfismo, y del núcleo y de la imagen del homomorfismo.
Para los grupos, el teorema afirma:
- Sean G y H grupos; sea f: G -> H un homomorfismo de grupos; sea K el núcleo de f; sea φ el homomorfismo sobreyectivo natural G -> G/K. Entonces existe un homomorfismo único h: G/K -> H tales que f = h.φ. Por otra parte, h es inyectivo y proporciona un isomorfismo entre G/K y la imagen de f.
La situación es descrita por el diagrama conmutativo siguiente:
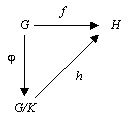
Teoremas similares son válidos para los espacios vectoriales, los módulos, y los anillos.
Categorías: Álgebra abstracta | Teoremas de álgebra
Wikimedia foundation.
2010.
Mira otros diccionarios:
Teorema fundamental sobre homomorfismos — En álgebra abstracta, para un número de estructuras algebraicas, el teorema fundamental sobre homomorfismos relaciona la estructura de dos objetos entre los cuales se dé un homomorfismo, y del núcleo y de la imagen del homomorfismo. Para los… … Enciclopedia Universal
Álgebra de Lie — En matemática, un álgebra de Lie es la estructura algebraica que describe un conjunto de transformaciones infinitesimales. Su uso principal reside en el estudio de objetos geométricos tales como grupos de Lie y variedades diferenciables. El… … Wikipedia Español
Grupo cociente — En teoría de grupos, dado un grupo G y un subgrupo normal N de G, el grupo cociente o grupo factor de G sobre N es, intuitivamente, el grupo que colapsa el grupo normal N al elemento neutro. El grupo cociente se denota por G/N, lo que normalmente … Wikipedia Español
Teoría de haces — En matemática, un haz F sobre un espacio topológico dado, X, proporciona, para cada conjunto abierto U de X, un conjunto F(U), de estructura más rica. A su vez dichas estructuras: F(U), son compatibles con la operación de restricción desde un… … Wikipedia Español
Geometría algebraica — La geometría algebraica es una rama de la matemática que, como sugiere su nombre, combina el álgebra abstracta, especialmente el álgebra conmutativa, con la geometría. Se puede comprender como el estudio de los conjuntos de soluciones de los… … Wikipedia Español
Anillo local — Saltar a navegación, búsqueda En Álgebra abstracta, los anillos locales son ciertos anillos comparativamente simples y que sirven para describir el comportamiento local de las funciones definidas sobre variedades algebraicas o variedades… … Wikipedia Español
Topología algebraica — La Topología algebraica es una rama de la matemática en la que se usan las herramientas del Álgebra abstracta para estudiar los espacios topológicos. Contenido 1 El método de los invariantes algebraicos 2 Resultados en homología 3 … Wikipedia Español

