Teoría de van Hiele

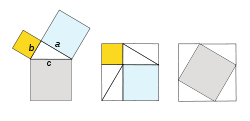Los cuadrados compuestos en el centro y a la derecha tienen áreas equivalentes. Quitándoles los triángulos el teorema de Pitágoras queda demostrado.

La Teoría de van Hiele o Modelo de van Hiele o Niveles van Hiele es una teoría de enseñanza y aprendizaje de la geometría, diseñado por el matrimonio holandés van Hiele.

El modelo tiene su origen en 1957, en las disertaciones doctorales de Dina van Hiele-Geldof y Pierre van Hiele en la Universidad de Utrecht, Holanda. El libro original donde se desarrolla la teoría es Structure and Insight : A theory of mathematics education.^[1]

La teoría se encasilla dentro de la didáctica de la matemática y específicamente en la didáctica de la Geometría

Ideas básicas de la teoría

La idea básica del modelo, expresado en forma sencilla es:

• El aprendizaje de la geometría se hace pasando por niveles de pensamiento.

Estos niveles no van asociados a la edad, y cumplen las siguientes características:

• No se puede alcanzar el nivel n sin haber pasado por nivel anterior n-1, o sea, el progreso de los alumnos a través de los niveles es invariante.

• En cada nivel de pensamiento, lo que era implícito, en el nivel siguiente se vuelve explicito.

• Cada nivel tiene su lenguaje utilizado (símbolos lingüísticos) y su significatividad de los contenidos (conexión de estos símbolos dotándolos de significado).

• Dos estudiantes con distinto nivel no pueden entenderse.

Niveles

Los niveles van Hiele son cinco, se suelen nombrar con números del 1 a 5, siendo esta notación la más utilizada; aunque también existe la notación del 0 al 4.

Nivel 0 : Visualización o Reconocimiento
Nivel 1 : Análisis
Nivel 2 : Ordenación o clasificación
Nivel 3 : Deducción Formal
Nivel 4 : Rigor

Nivel 0

En este nivel los objetos se perciben en su totalidad como un todo, no diferenciando sus características y propiedades.

Las descripciones son visuales y tendientes a asemejarlas con elementos familiares.

Ejemplo: identifica paralelogramos en un conjunto de figuras. Identifica ángulos y triángulos en diferentes posiciones en imágenes.

Nivel 1

Se perciben propiedades de los objetos geométricos. Pueden describir objetos a través de sus propiedades (ya no solo visualmente). Pero no puede relacionar las propiedades unas con otras.

Ejemplo: un cuadrado tiene lados iguales. Un cuadrado tiene ángulos iguales

Nivel 2

Describen los objetos y figuras de manera formal. Entienden los significados de las definiciones. Reconocen como algunas propiedades derivan de otras. Establecen relaciones entre propiedades y sus consecuencias.

Los estudiantes son capaces de seguir demostraciones. Aunque no las entienden como un todo, ya que, con su razonamiento lógico solo son capaces de seguir pasos individuales.

Ejemplo: en un paralelogramo, lados opuestos iguales implican lados opuestos paralelos. Lados opuestos paralelos implican lados opuestos iguales.

Nivel 3

En este nivel se realizan deducciones y demostraciones. Se entiende la naturaleza axiomática y se comprende las propiedades y se formalizan en sistemas axiomáticos.

Van Hiele llama a este nivel la esencia de la matemática

Ejemplo: demuestra de forma sintética o analítica que las diagonales de un paralelogramo se cortan en su punto medio.

Nivel 4

Se trabaja la geometría sin necesidad de objetos geométricos concretos. Se conoce la existencia de diferentes sistemas axiomáticos y se puede analizar y comparar.

Se aceptará una demostración contraria a la intuición y al sentido común si el argumento es valido.

Dado que el nivel 5 se piensa que es inalcanzable para los estudiantes y muchas veces se prescinde de él, además, trabajos realizados señalan que los estudiantes no universitarios, como mucho, alcanzan los tres primeros niveles. Es importante señalar que, un o una estudiante puede estar, según el contenido trabajado, en un nivel u otro distinto.

Enlaces externos

Modelo de Van Hiele para la didáctica de la Geometría

Apuntes para la enseñanza de la Geometría

Aplicación del modelo propuesto en la Teoría de Van Hiele para la enseñanza de la geometría

Referencias bibliográficas

1. Huerta Palau, Manuel Pedro (9 de 1999) (en español). Los niveles de Van Hiele en relación con la taxonomía SOLO y los mapas conceptuales (1 edición). Universidad de Valencia. Servicio de Publicaciones. ISBN 978-84-370-3907-7. 
2. Guillén Soler, Gregoria (9 de 1999) (en español). El modelo Van Hiele aplicado a la geometría de los sólidos : observación de procesos de aprendizaje (1 edición). Universidad de Valencia. Servicio de Publicaciones. ISBN 978-84-370-3901-5. 
3. Arieta-Araunabeña Martínez, Mikel; Lacalle López, Mari Cruz; López Roldán, Milagros (5 de 1997) (en español). Tratamientos de la diversidad en geometría : el modelo de Van-Hiele (1 edición). País Vasco. Dirección de Renovación Pedagógica. pp. 136. ISBN 978-84-89845-93-0. 
4. (en español) Diseño y evaluación de una propuesta curricular de aprendizaje de la geometría en enseñanza secundaria basada en el modelo de razonamiento de Van Hiele (1 edición). Ministerio de Educación, Política Social y Deporte . Subdirección General de Información y Publicaciones. 11 de 1994. pp. 202. ISBN 978-84-369-2539-5. 
5. Jaime Pastor, Adela (12 de 1993) (en español). Aportaciones al modelo de Van Hiele : la enseñanza de las isometrías (1 edición). Universidad de Valencia. Servicio de Publicaciones. ISBN 978-84-370-1429-6. 
6. Corberán Salvador, Rosa María (7 de 1989) (en español). Didáctica de la geometría : modelo Van Hiele (1 edición). Universidad de Valencia. Servicio de Publicaciones. pp. 100. ISBN 978-84-370-0523-2. 

Referencias