Teorema de Pitágoras

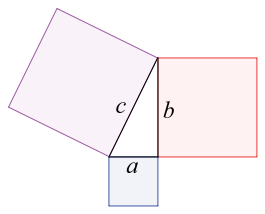
El Teorema de Pitágoras establece que en un triángulo rectángulo, el área del cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de las áreas del cuadrado de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).

Teorema de Pitágoras

En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Pitágoras de Samos

Si un triángulo rectángulo tiene catetos de longitudes $a \,$ y $b \,$ , y la medida de la hipotenusa es $c \,$ , se establece que:

(1) $c^2 = b^2 + a^2 \,$

De la ecuación (1) se deducen fácilmente 3 corolarios de aplicación práctica:

**Pitágoras ( c²=a²+b² ) – Fórmulas prácticas**
$a = +\sqrt {c^2 - b^2}$	$b= +\sqrt{c^2-a^2}$	$c = +\sqrt {a^2 + b^2}$

Historia

El Teorema de Pitágoras lleva este nombre porque su descubrimiento recae sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.

Designaciones convencionales

**Triángulos — Resumen de convenciones de designación**
Vértices	$A$	$B$	$C$
*Lados (como segmento)*	$BC$	$AC$	$AB$
*Lados (como longitud)*	$a$	$b$	$c$
Ángulos	$\widehat{\alpha} = \widehat{a} = \widehat{A} = \widehat{BAC}$	$\widehat{\beta} = \widehat{b} = \widehat{B} = \widehat{ABC}$	$\widehat{\gamma} = \widehat{c} = \widehat{C} = \widehat{ACB}$

Demostraciones

El Teorema de Pitágoras es de los que cuenta con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de Magíster matheseos.

Algunos autores proponen hasta más de mil demostraciones. Otros autores, como el matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927 The Pythagorean Proposition.

En ese mismo libro, Loomis clasificaría las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.

China: el Chou Pei Suan Ching, y el Chui Chang Suang Shu

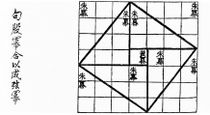
Prueba visual para un triángulo de a = 3, b = 4 y c = 5 como se ve en el Chou Pei Suan Ching, 500-200 a. C.

El Chou Pei es una obra matemática de datación discutida en algunos lugares, aunque se acepta mayoritariamente que fue escrita entre el 500 y el 300 a. C. Se cree que Pitágoras no conoció esta obra. En cuanto al Chui Chang parece que es posterior, está fechado en torno al año 250 a. C.

El Chou Pei demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro triángulos de base a y altura b, y un cuadrado de lado c.

Demostración

Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:

$a^2 + b^2 = c^2\,$

Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:

$(a-b)^2 = a^2 - 2ab + b^2 \,$

Ya que $(b-a)^2 = (a-b)^2 \,$ .

Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:

$c^2 = 4 \cdot \left( \frac{a \cdot b}{2} \right) + a^2 - 2ab + b^2= a^2 + b^2$

Con lo cual queda demostrado el teorema.

Demostraciones supuestas de Pitágoras

Se cree que Pitágoras se basó en la semejanza de los triángulos ABC, AHC y BHC. La figura coloreada hace evidente el cumplimiento del teorema.

Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales.^[1]

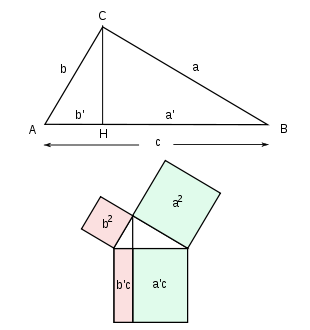
Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente.

Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.

De la semejanza entre ABC y AHC:

y dos triángulos son semejantes si hay dos o más ángulos congruentes.

$\frac {b}{b'}=\frac {c}{b}$

$b^2\ =\ b'c$

De la semejanza entre ABC y BHC:

$\frac {a}{a'}=\frac {c}{a}$

$a^2\ =\ a'c$

Los resultados obtenidos son el teorema del cateto. Sumando:

$a^2\ +\ b^2 =a'c\ +\ b'c\ =\ c\left (a'+b'\right )$

Pero $\left (a'+b'\right )=\ c$ , por lo que finalmente resulta:

$a^2\ +\ b^2 =c^2$

La relación entre las superficies de dos figuras semejantes es igual al cuadrado de su razón de semejanza. En esto pudo haberse basado Pitágoras para demostrar su teorema

Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.

Los triángulos PQR y PST son semejantes, de manera que:

$\frac {r}{u}=\frac {s}{v} = r$

siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:

$S_{PQR}\ =\ \frac {1}{2} \left ( rs \right )$

$S_{PST}\ =\ \frac {1}{2} \left ( uv \right )$

obtenemos después de simplificar que:

$\frac {S_{PQR}}{S_{PST}}=\frac {rs}{uv} = \frac {r}{u} \cdot \frac {s}{v}$

pero siendo $\frac {r}{u}=\frac {s}{v} = r$ la razón de semejanza, está claro que:

$\frac {S_{PQR}}{S_{PST}}= \left (\frac {r}{u} \right )^2 = \left ( \frac {s}{v} \right ) ^2$

Es decir, "la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".

Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:

$\frac {S_{ACH}}{S_{BCH}}= \left (\frac {b}{a} \right )^2$

que de acuerdo con las propiedades de las proporciones nos da:

$\frac {S_{ACH}} {b^2} = \frac {S_{BCH}} {a^2} = \frac {S_{ACH} + S_{BCH}}{b^2+a^2 }$ (I)

y por la semejanza entre los triángulos ACH y ABC resulta que:

$\frac {S_{ACH}}{S_{ABC}}= \left (\frac {b}{c} \right )^2$

$\frac {S_{ACH}}{b^2} = \frac {S_{ABC}} {c^2}$

pero según (I) $\frac {S_{ACH}} {b^2} = \frac {S_{ACH} + S_{BCH}}{b^2+a^2 }$ , así que:

$\frac {S_{ACH} + S_{BCH}}{b^2+a^2 } = \frac {S_{ABC}} {c^2}$

y por lo tanto:

$b^2 \ +\ a^2 \ = \ c^2$

quedando demostrado el teorema de Pitágoras.

Los cuadrados compuestos en el centro y a la derecha tienen áreas equivalentes. Quitándoles los triángulos el teorema de Pitágoras queda demostrado.

Es asimismo posible que Pitágoras hubiera obtenido una demostración gráfica del teorema.

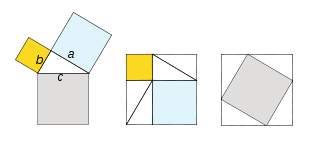
Partiendo de la configuración inicial, con el triángulo rectángulo de lados a, b, c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados diferentes:

Uno de ellos –centro- está formado por los cuadrados de los catetos, más cuatro triángulos rectángulos iguales al triángulo inicial.
El otro cuadrado –derecha- lo conforman los mismos cuatro triángulos, y el cuadrado de la hipotenusa.

Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris ( $c 2$ ) equivale a la de los cuadrados amarillo y azul ( $b 2 + a 2$ ), habiéndose demostrado el teorema de Pitágoras.

Demostración de Euclides: proposición I.47 de Los Elementos

Figura Euclides 1: La proposición I.41^[2] de Euclides. La superficie del rectángulo ABCD es el doble de la de cualquiera de los triángulos: sus bases son la misma –DC-, y están entre las mismas paralelas. Esto es cuanto necesita Euclides para demostrar el teorema de Pitágoras.

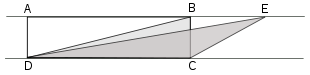
Figura Euclides 2: La proposición I.36^[3] de Euclides: los paralelogramos ABCD y EFCD tienen áreas equivalentes, por tener igual base, y estar comprendidos entre las mismas paralelas.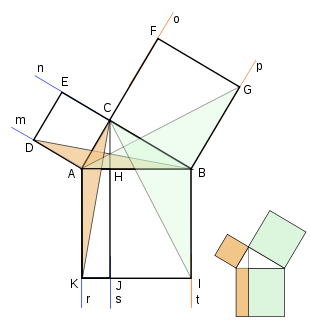

Figura Euclides 3: La demostración de Euclides es puramente geométrica. Su columna vertebral es la sencilla proposición I.41^[2] de Los Elementos.

El descubrimiento de los números irracionales por Pitágoras y los Pitagóricos supuso un contratiempo muy serio.^[4] De pronto, las proporciones dejaron de tener validez universal, no siempre podían aplicarse. La demostración de Pitágoras de su teorema se basaba muy probablemente en proporciones, y una proporción es un número racional. ¿Sería realmente válida como demostración? Ante esto, Euclides elabora una demostración nueva que elude la posibilidad de encontrarse con números irracionales.

El eje de su demostración es la proposición I.47^[5] de Los Elementos:

En los triángulos rectángulos el cuadrado del lado opuesto al ángulo recto es igual a la suma de los cuadrados de los lados que comprenden el ángulo recto.

Euclides (proposición I.47)

Basándose en la proposición I.41^[2] de Los Elementos, que equivale a decir que a igual base y altura, el área del paralelogramo dobla a la del triángulo, (véase Figura Euclides 1).

Se tiene el triángulo ABC, rectángulo en C (véase Figura Euclides 3), y se construye los cuadrados correspondientes a catetos e hipotenusa. La altura CH se prolonga hasta J. Seguidamente se traza cuatro triángulos, iguales dos a dos:

Triángulos ACK y ABD: son iguales, pues siendo AD=AC, y AK=AB, necesariamente BD=CK. Sus tres lados son iguales.
Triángulos ABG y CBI: análogamente, AB=BI, y BG=BC, así que AG=CI. Sus tres lados son asimismo iguales.

Abundando en las anteriores consideraciones, nótese que un giro con centro en A, y sentido positivo, transforma ACK en ABD. Y un giro con centro en B, y sentido también positivo, transforma ABG en CBI. En la demostración de Leonardo da Vinci se encontrará nuevamente con giros que demuestran la igualdad de figuras.

Véase (en la Figura Euclides 3) que:

Las paralelas r y s comprenden al triángulo ACK y el rectángulo AHJK, los cuales tienen la misma base, AK. Por tanto de acuerdo con la proposición I.41^[2] de Los Elementos, AHJK tiene doble área que ACK, (véase Figura Euclides 1).
Las paralelas m y n contienen a ABD y ADEC, cuya base común es AD. Así que el área de ADEC es doble de la de ABD.

Pero siendo ACK=ABD, resulta que el rectángulo AHJK y el cuadrado ADEC tienen áreas equivalentes. Haciendosé razonamientos similares con los triángulos ABG y CBI, respecto al cuadrado BCFG y al rectángulo HBIJ respectivamente, se concluye que éstos últimos tienen asimismo áreas iguales. A partir de lo anterior, surge de inmediato que: "la suma de las áreas de los cuadrados construidos sobre los catetos, es igual al área del cuadrado construido sobre la hipotenusa".

Demostración de Pappus

La proposición I.36^[3] de Euclides: los paralelogramos ABCD y EFCD tienen áreas equivalentes, por tener igual base, y estar comprendidos entre las mismas paralelas.

La demostración de Pappus parece ser unas musicales variaciones sobre un mismo tema, respecto a la de Euclides.

Unos 625 años después que Euclides, Pappus^[6] parece seguir su senda, y desarrolla una demostración del teorema de Pitágoras basada en la proposicón I.36^[3] de Los Elementos de Euclides:

Dos paralelogramos de igual base, y entre las mismas paralelas, tienen superficies equivalentes.

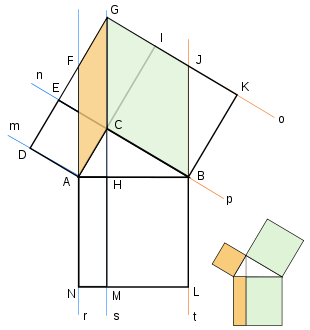
Partimos del triángulo ABC rectángulo en C, sobre cuyos catetos e hipotenusa hemos construido los cuadrados correspondientes.

Prolongando CH hacia arriba se obtiene el rectángulo CEGI cuya diagonal CG determina en aquél dos triángulos rectángulos iguales al triángulo ABC dado:

Los ángulos agudos GCI y ABC tienen sus lados perpendiculares
El lado CI es igual al lado CB

En consecuencia los triángulos rectángulos ABC, ICG y EGC tienen sus tres lados iguales.

Los paralelogramos ACGF y AHMN tienen la misma base CG=HM, y están comprendidos entre las mismas paralelas, r y s. Por lo tanto tienen la misma superficie (Elementos I.36)
Aplicando el mismo principio a ACGF y ACED –base común AC, y paralelas m y n- resulta que ambos paralelogramos tienen superficies asimismo equivalentes.

De 1) y 2) se sigue que las superficies de ACED y AHMN son iguales.

Análogamente:

CGJB y BLMH tienen la misma base CG=MH, y están comprendidos entre las paralelas s y t. Sus superficies son equivalentes.
CGJB y CIKB tienen base común CB, y están entre las paralelas o y p. Sus superficies son iguales.

De dónde se deduce la equivalencia de las superficies de BLMH y de CIKB.

El teorema de Pitágoras queda demostrado.

Demostración de Bhaskara

Bhaskara desarrolla una demostración gráfica y algebraica del teorema de Pitágoras.

Bhaskara II, el matemático y astrónomo hindú del siglo XII, nos da la siguiente demostración del teorema de Pitágoras.

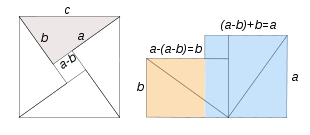
Con cuatro triángulos rectángulos de lados a, b y c se construye el cuadrado de lado c –izquierda-, en cuyo centro se forma otro cuadrado de lado (a-b).

Redistribuyendo los cuatro triángulos y el cuadrado de lado (a-b), construimos la figura de la derecha, cuya superficie resulta ser la suma de la de dos cuadrados: uno de lado a –azul- y otro de lado b -naranja-.

Se ha demostrado gráficamente que $c 2 = a 2 + b 2$

Algebraicamente: el área del cuadrado de lado c es la correspondiente a los cuatro triángulos, más el área del cuadrado central de lado (a-b), es decir:

$c^2=4 \cdot \frac {ab}{2}+ (a-b)^2$

expresión que desarrollada y simplificada nos da el resultado $c 2 = a 2 + b 2$ , y el teorema queda demostrado.

Demostración de Leonardo da Vinci

El diseño inicial, con el triángulo y los cuadrados de catetos e hipotenusa, es modificado por Leonardo da Vinci al añadir dos triángulos iguales al ABC: el ECF y el HIJ.

En el elenco de inteligencias que abordaron el teorema de Pitágoras no falta el genio del Renacimiento, Leonardo da Vinci.

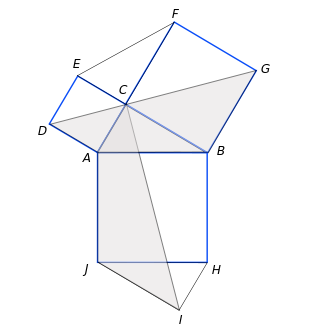
Partiendo del triángulo rectángulo ABC con los cuadrados de catetos e hipotenusa, Leonardo añade los triángulos ECF y HIJ, iguales al dado, resultando dos polígonos, cuyas superficies va a demostrar que son equivalentes:

Polígono ADEFGB: la línea DG lo divide en dos mitades idénticas, ADGB y DEFG.
Polígono ACBHIJ: la línea CI determina CBHI y CIJA.

Comparemos los polígonos destacados en gris, ADGB y CIJA:

De inmediato vemos que tienen tres lados iguales: AD=AC, AB=AJ, BG=BC=IJ
Asimismo es inmediata la igualdad entre los ángulos de los siguientes vértices:
- A de ADGB y A de CIJA
- B de ADGB y J de CIJA

Se concluye que ADGB y CIJA son iguales.

De modo análogo se comprueba la igualdad entre ADGB y CBHI.

Además, de un modo semejante a lo explicado en la demostración de Euclides, nótese que un giro de centro A, y sentido positivo, transforma CIJA en ADGB. Mientras que un giro de centro B, y sentido negativo, transforma CBHI en ADGB.

Todo ello nos lleva a que los polígonos ADEFGB y ACBHIJ tienen áreas equivalentes. Pues bien, si a cada uno le quitamos sus dos triángulos –iguales- las superficies que restan forzosamente serán iguales. Y esas superficies no son sino los dos cuadrados de los catetos en el polígono ADEFGB, por una parte, y el cuadrado de la hipotenusa en el polígono ACBHIJ, por la otra. El teorema de Pitágoras queda demostrado.

Demostración de Garfield

El polígono construido por Garfield es un trapecio de bases a y b, compuesto por tres triángulos rectángulos.

James Abram Garfield (1831-1881), el vigésimo Presidente de los Estados Unidos,^[7] desarrolló una demostración del teorema de Pitágoras publicada en el New England Journal of Education.

Garfield construye un trapecio de bases a y b, y altura (a+b), a partir del triángulo rectángulo de lados a, b y c. Dicho trapecio resulta compuesto por tres triángulos rectángulos: dos iguales al dado, y un tercero, isósceles de catetos c. En consecuencia:

(g.1) $S_{trapecio}=\frac {a+b}{2} \cdot (a+b)$

como corresponde a la superficie del trapecio, pero asimismo tenemos una figura compuesta por tres triángulos, dos de ellos iguales, de modo que:

(g.2) $S=2 \cdot \frac {ab}{2} + \frac {c^2}{2}$

igualando la ecuación (g.2) con la (g.1) obtenemos:

$(ab) + \frac {c^2}{2} = \frac {1}{2} (a+b) \cdot (a+b)$

pasando el $1 / 2$ al otro miembro y simplificando ...

2 a b + c 2 = (a + b) 2

expandiendo el miembro derecho ...

2 a b + c 2 = a 2 + 2 a b + b 2

restando $2 a b$ a ambos miembros, finalmente nos da:

$c 2 = a 2 + b 2$

y el teorema está demostrado.

Véase también

Notas

↑ Una vez descubiertos los números irracionales esta demostración quedaba invalidada. Será Euclides el primero en prescindir de la proporcionalidad para demostrar el teorema.
↑ ^a ^b ^c ^d Euclides Los Elementos, proposición I.41 → "Si un paralelogramo tiene la misma base que un triángulo y está contenido entre las mismas paralelas, el paralelogramo es el doble del triángulo".
↑ ^a ^b ^c Euclides Los Elementos, proposición I.36 → "Los paralelogramos que tienen las bases iguales y están contenidos entre las mismas paralelas, son iguales entre sí".
↑ Los pitagóricos habían llegado a la conclusión de que el número racional lo explicaba todo. Por eso el descubrimiento de los números irracionales causó un verdadero trauma. Juraron mantener el secreto de lo descubierto pero, según la leyenda (¿o realidad?) el pitagórico Hipaso de Metaponto lo reveló. En represalia, sus compañeros invocaron la ira de los dioses e Hipaso murió en un naufragio.
↑ Euclides Los Elementos, proposición I.47 → "En los triángulos rectángulos el cuadrado del lado opuesto al ángulo recto es igual a la suma de los cuadrados de los lados que comprenden el ángulo recto".
↑ Pappus nació en Alejandría -Pappus de Alejandría- sobre el año 290, y murió alrededor del 350. Es el último de los grandes geómetras griegos.
↑ James A. Garfield murió el 19 de septiembre de 1881, a consecuencia de un atentado sufrido el 2 de julio del mismo año. Fue el segundo Presidente asesinado, después de Abraham Lincoln. Su demostración del teorema de Pitágoras es de 1876, cuando era miembro de la Cámara de Representantes.

Bibliografía

PLATÓN: Diálogos. Menexenos-Menon-Kratilos-Faidros. Ediciones Ibéricas. Madrid, 1958
PAUL STRATHERN: Pitágoras y su teorema. Siglo XXI de España Editores. Madrid, 1999
LOOMIS E. S.: The Pythagorean Proposition. NCTM. Míchigan, 1940
GONZÁLEZ URBANEJA, P. M.: Pitágoras. El filósofo del número. Nivola. Madrid, 2001
Martínez Delgado, Alberto. Teorema de Pitágoras: originalidadde las demostraciones de E. García Quijano (1848). http://www.rsme.es/gacetadigital/abrir.php?id=262. Consultado el 4 de octubre de 2010.

Enlaces externos

Wikimedia Commons alberga contenido multimedia sobre Teorema de Pitágoras. Commons

Categorías:

Teoremas de geometría
Triángulos
Geometría elemental

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Teorema de Pitágoras — El Teorema de Pitágoras establece que en un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa: Este teorema fue propuesto por Pitágoras de Samos (582 adC 496 adC), un filósofo y matemático griego … Enciclopedia Universal
Pitágoras — Saltar a navegación, búsqueda Pitágoras (Πυθαγόρας) Busto de Pitágoras de Samos en los Museos Capitolinos, Roma … Wikipedia Español
Pitágoras — V. «tabla de Pitágoras». * * * Pitágoras de Samos (en griego Πυθαγόρας ο Σάμιος) (582 adC 496 adC) fue un filósofo y matemático griego, famoso sobre todo por el Teorema de Pitágoras. Pitágoras, «el padre de los números», nació en la isla de Samos … Enciclopedia Universal
Teorema del seno — Teorema del seno. En trigonometría, el teorema del seno es una relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos. Usualmente se presenta de la siguiente forma … Wikipedia Español
Teorema del coseno — El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente, en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado … Wikipedia Español
Teorema de De Gua — El teorema de De Gua, llamado así en honor al matemático francés Jean Paul de Gua de Malves, es un análogo en tres dimensiones del teorema de Pitágoras. Este teorema establece que si un tetraedro posee un vértice formado por ángulos rectos (como… … Wikipedia Español
Teorema — (Del gr. theorema, meditación.) ► sustantivo masculino 1 LÓGICA Proposición que afirma una verdad demostrable a través de un razonamiento. 2 LÓGICA, MATEMÁTICAS Expresión de un sistema formal, demostrable en el interior de dicho sistema. * * *… … Enciclopedia Universal
Teorema de Apolonio — fig.1: Esquema con áreas → ( ). En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona … Wikipedia Español
Teorema de la altura — En matemáticas, el teorema de la altura de un triángulo rectángulo establece que: Teorema de la altura (forma 1) En cualquier triángulo rectángulo la altura relativa a la hipotenusa es la media proporcional entre las proyecciones ortogonales de… … Wikipedia Español
Teorema del cateto — Figura 1 Los segmentos m y n son las respectivas proyecciones de los lados b y a sobre la hipotenusa c, siendo h la altura correspondiente a la hipotenusa. El teorema del cateto establece lo siguiente … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Teorema de Pitágoras

Contenido

Historia

Designaciones convencionales

Demostraciones