Conjetura de Collatz

La conjetura de Collatz, conocida también como conjetura 3n+1 o conjetura de Ulam (entre otros nombres), fue enunciada por el matemático Lothar Collatz en 1937, y a la fecha no se ha resuelto.

Enunciado

Tiempo de órbita (número de iteraciones) necesario para alcanzar la unidad para números comprendidos entre 1 y 13000.

Cota superior para valores entre 1 y 1300. La línea horizontal superior corresponde a la cota 9232. Esta cota es un valor 'preferido' para muchas secuencias, como las que comienzan con 27, 31, 41, 47, 54, 55, 62, 63, etc.

Sea la siguiente operación, aplicable a cualquier número entero positivo:

• Si el número es par, se divide entre 2.
• Si el número es impar, se multiplica por 3 y se suma 1.

Formalmente, esto equivale a una función :

Dado un número cualquiera, podemos considerar su órbita, es decir, las imágenes sucesivas al iterar la función. Por ejemplo, si n=13:

Si observamos este ejemplo, la órbita de 13 es periódica, es decir, se repite indefinidamente a partir de un momento dado):

13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1,...

La conjetura dice que siempre alcanzaremos el 1 (y por tanto el ciclo 4, 2, 1) para cualquier número con el que comencemos. Ejemplos:

• Comenzando en n = 6, uno llega a la siguiente sucesión: 6, 3, 10, 5, 16, 8, 4, 2, 1.
• Empezando en n = 11, la sucesión tarda un poco más en alcanzar el 1: 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
• Empezando n = 27, la sucesión tiene 112 pasos, llegando hasta 9232 antes de descender a 1: 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1.

Implementación en C

Esta sería la implementación en C de la conjetura, escrito como una función que toma como argumentos el primer valor:

void collatz(long int n)
{
        while(n>1)
        {
                printf("%d",n);
                if ((n%2)==1)
                        n=3*n+1;
                else
                        n=n/2;
        }
        printf("%d",n);
}

Estado actual del problema

Aunque no se ha demostrado la veracidad ni falsedad del resultado, existen ciertas evidencias en ambos sentidos^{[cita requerida]}.

Si existe algún contraejemplo a la conjetura (es decir, un número cuya secuencia no alcance nunca el 1), debe satisfacer alguna de estas condiciones:

• la órbita del número no está acotada; o bien
• la órbita también es periódica, pero con un período distinto de 4, 2, 1.

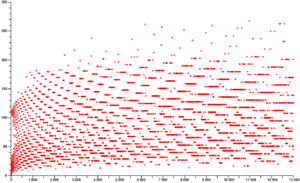
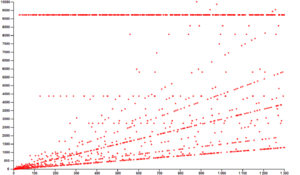
Evidencia computacional

Aunque formalmente no demuestra nada, existen diversos grupos de computación que se dedican a calcular las secuencias de números cada vez más grandes. En Noviembre de 2005 se comprobó la conjetura para todas las secuencias de números menores que 2⁵⁸. Esta es una evidencia intuitiva fuerte a favor de la veracidad del resultado, a pesar de no aportar nada formalmente hablando.

Resultados parciales

1. Los números que son suma de potencias de 2 exponente par, como 5 = 1 + 4, 21 = 1 + 4 + 16, 53 = 1 + 4 + 16 + 32, 85 = 1 + 4 + 16 + 64 generan el 1 en forma casi directa, como en el ejemplo:

21 · 3 + 1 = 64, que es una potencia de 2 y genera el 1 al dividir 6 veces entre 2.

2. Al agregar un 3 al final a estos números (a partir del 1, el 13, a partir del 5, el 53, a partir del 21, el 213, a partir del 85, el 853, etc), se obtiene 5, a partir del cual se obtiene 1.

213 = 210 + 3

213 · + 1 = 210 · 3 + 3 · 3 + 1 = 630 + 10 = 640 = 5 · 128

128 es una potencia de 2, por lo que, dividiendo 7 veces entre 2, se llega a 5.

3. Los números que son de la forma (2ⁿ)² + 1 generan 3ⁿ + 1 y estos son menores que el número de partida para todo n natural.

4. Los números que son de la forma 3 mod 6 pueden considerarse como generadores de números mayores. Por ejemplo, el 31 puede generarse partiendo del 27. De la misma forma, el 111 genera el 334 que pertenece a la sucesión de números que empieza en el 27

Se ha propuesto el estudio de patrones en sistema binario para el estudio de las propiedades de los números expresados como polinomios de potencias de 2, lo que simplifica el estudio de las propiedades de los mismos. Luego pueden ser demostrados los teoremas correspondientes. Por ejemplo, los números como 5, 21, 53, 85, etc., tienen una expresión del tipo 10101..01 en sistema binario. Esos números son, entonces, los coeficientes de un polinomio en potencias pares de 2.

Los números del tipo 111...11 (n unos) que son iguales a 2ⁿ − 1, generan en un primer momento los de este tipo: 1011...111, (n+1 cifras). En un segundo momento se obtiene 10001...1 (n+2 cifras), luego 11010111...1, etc.

Enlaces externos

• Información actualizada sobre cálculos (en inglés)
• Web de un investigador que busca una demostración (en inglés)
• Artículo de revisión sobre el tema (en inglés)
• Método recursivo del algoritmo en PHP
• Implementación del algoritmo en PHP
• Proyecto BOINC, que usa el poder de calculo de las GPU´s (Ati, Nvidia) y de CPU, para encontrar la solución a este problema (en ingles)