Método del punto fijo

Método del punto fijo
Los dos puntos fijos, marcados en rojo, de la función f(x) = x2 − 4

El método del punto fijo es un método iterativo que permite resolver sistemas de ecuaciones no necesariamente lineales. En particular se puede utilizar para determinar raíces de una función de la forma f(x), siempre y cuando se cumplan los criterios de convergencia.

Contenido

Descripción del Método

El método de iteración de punto fijo, también denominado método de aproximación sucesiva, requiere volver a escribir la ecuación f(x) = 0 en la forma

x = g(x).

Procedimiento

El procedimiento empieza con una estimación o conjetura inicial de x, que es mejorada por iteración hasta alcanzar la convergencia. Para que converja, la derivada (dg / dx) debe ser menor que 1 en magnitud (al menos para los valores x que se encuentran durante las iteraciones). La convergencia será establecida mediante el requisito de que el cambio en x de una iteración a la siguiente no sea mayor en magnitud que alguna pequeña cantidad €.

Algoritmo para iteración de punto fijo

1. Se ubica la ráiz de f(x) analizando la gráfica.

2. Se obtiene un despeje x = g(x) de la función.

3. Obtenemos de x = g(x) su derivada g\prime(x).

4. Resolviendo la desigualdad -1 ≤ g\prime(x) ≤ 1 obtenemos el rango de valores en los cuales esta el punto fijo llamado R.

5. Con R buscamos la raíz en g(x), es decir g(R) = R haciendo iteración de las operaciones.


Ejemplo 1

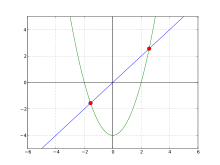
Sea f(x) = x2 − 5x + 3 una función, encuentre la raíz.

Ubicamos la ráiz analizando la gráfica.

Pfijo1

Obtenemos x = g(x):

x= \sqrt{5x-3}

Después obtenemos la derivada de la función:

{dg \over dx}={5 \over 2\sqrt{5x-3}}

Entonces resolvemos las desigualdades:

{5 \over 2\sqrt{5x-3}}<1

La solución es:

({37 \over 20},\infty)

{5 \over 2\sqrt{5x-3}}>-1

La solución es:

({3 \over 5},\infty)

O visto de otra manera, vemos que en la grafica de la derivada existen valores entre -1 y 1:

Pfijo2

Ya que se tienen los valores del rango R, encontramos la raíz haciendo la iteración de las operaciones:

Pfijo3

En la tabla se puede ver el valor que en este caso se uso de R, la iteración consiste en usar ese valor en x = g(x) para obtener los siguientes valores haciendo la misma operación usando el valor anterior.

Después de un número considerable de iteraciones obtenemos la raíz en 4.30268775.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Teorema del punto fijo de Banach — En análisis matemático el teorema del punto fijo de Banach (también llamado teorema de la aplicación contractiva) es una de las herramientas más importantes para demostrar la existencia de soluciones de numerosos problemas matemáticos. El teorema …   Wikipedia Español

  • Método de Steffensen — El método de Steffensen (por Johan Frederik Steffensen) es un algoritmo para obtener los ceros de una función. El método de Steffensen se puede considerar como una combinación del método de punto fijo y del método de Aitken. Como el método de… …   Wikipedia Español

  • Método de la secante — Dos primeras iteraciones del método de la secante. En análisis numérico el método de la secante es un método para encontrar los ceros de una función de forma iterativa. Es una variación del método de Newton Raphson donde en vez de calcular la… …   Wikipedia Español

  • Método de Newton — En análisis numérico, el método de Newton (conocido también como el método de Newton Raphson o el método de Newton Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado …   Wikipedia Español

  • Método de Hartree-Fock — El método de Hartree Fock (HF) es una forma aproximada de las ecuaciones de mecánica cuántica para fermiones, utilizada en física y química (donde también se conoce como método de campo autoconsistente). Esto se debe a que sus ecuaciones, basadas …   Wikipedia Español

  • Método iterativo — En matemática computacional, un método iterativo trata de resolver un problema (como una ecuación o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con …   Wikipedia Español

  • Método de la velocidad relativa — Es un método utilizado para calcular la velocidad absoluta de un punto a partir de su velocidad relativa a otro punto de velocidad conocida. Es muy común utilizarlo en cursos de ingeniería mecánica para obtener la velocidad de una barra, pistón u …   Wikipedia Español

  • Método de Jacobi — En análisis numérico el método de Jacobi es un método iterativo, usado para resolver sistemas de ecuaciones lineales del tipo Ax = b. El algoritmo toma su nombre del matemático alemán Carl Gustav Jakob Jacobi. El método de Jacobi consiste en usar …   Wikipedia Español

  • Teoría del equilibrio general — Excedente de los consumidores y los productores en el punto de equilibrio para las curvas de oferta y demanda. La teoría del equilibrio general es una rama de la teoría microeconómica. La misma trata de dar una explicación global del… …   Wikipedia Español

  • Método de la regla falsa — En cálculo numérico, el método de regula falsi (regla falsa) o falsa posición es un método iterativo de resolución numérica de ecuaciones no lineales. El método combina el método de bisección y el método de la secante. Contenido 1 El método 2… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”