Método de Newton

En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.

Historia

El método de Newton fue descrito por Isaac Newton en De analysi per aequationes número terminorum infinitas (escrito en 1669, publicado en 1711 por William Jones) y en De metodis fluxionum et serierum infinitarum (escrito en 1671, traducido y publicado como Método de las fluxiones en 1736 por John Colson). Sin embargo, su descripción difiere en forma sustancial de la descripción moderna presentada más arriba: Newton aplicaba el método solo a polinomios, y no consideraba las aproximaciones sucesivas x_n, sino que calculaba una secuencia de polinomios para llegar a la aproximación de la raíz x. Finalmente, Newton ve el método como puramente algebraico y falla al no ver la conexión con el cálculo.

Isaac Newton probablemente derivó su método de forma similar aunque menos precisa del método de François Viète. La esencia del método de Viète puede encontrarse en el trabajo del matemático persa Sharaf al-Din al-Tusi.

El método de Newton-Raphson es llamado así por la razón de que el matemático inglés Joseph Raphson (contemporaneo de Newton) se hizo miembro de la Royal Society en 1691 por su libro aequationum universalis Análisis que publico en 1690 y el cual contenía este método para aproximar raíces. Mientras que Newton en su libro Método de las fluxiones describe el mismo método escrito en 1671, pero publicado hasta 1736, lo que significa que Raphson había publicado este resultado casi 50 años antes, aunque no fue tan popular como los trabajos de Newton y se le reconoció posteriormente.

Descripción del método

La función ƒ es mostrada en azul y la línea tangente en rojo. Vemos que x_n+1 es una mejor aproximación que x_n para la raíz x de la función f.

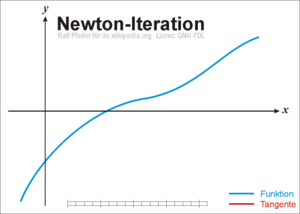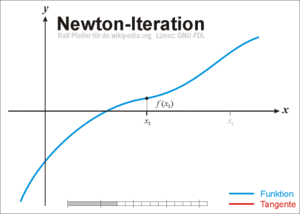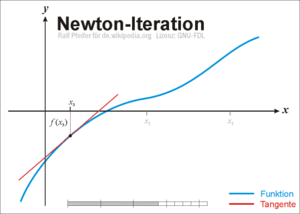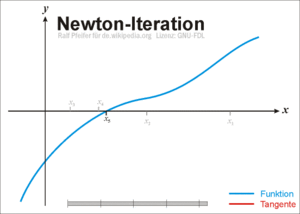
El método de Newton-Raphson es un método abierto, en el sentido de que su convergencia global no está garantizada. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente.

Sea f : [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x₀ y definimos para cada número natural n

Donde f ' denota la derivada de f.

Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita cognoscible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.

Obtención del Algoritmo

Tres son las formas principales por las que tradicionalmente se ha obtenido el algoritmo de Newton-Raphson.

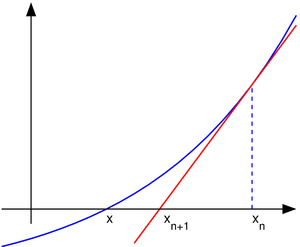
La primera de ellas es una simple interpretación geométrica. En efecto, atendiendo al desarrollo geométrico del método de la secante, podría pensarse en que si los puntos de iteración están lo suficientemente cerca (a una distancia infinitesimal), entonces la secante se sustituye por la tangente a la curva en el punto. Así pues, si por un punto de iteración trazamos la tangente a la curva, por extensión con el método de la secante, el nuevo punto de iteración se tomará como la abscisa en el origen de la tangente (punto de corte de la tangente con el eje X). Esto es equivalente a linealizar la función, es decir, f se reemplaza por una recta tal que contiene al punto (x₀, f (x₀)) y cuya pendiente coincide con la derivada de la función en el punto, f'(x₀). La nueva aproximación a la raíz, x₁, se logra la intersección de la función lineal con el eje X de abscisas. Matemáticamente:

Ilustración de una iteración del método de Newton (la función f se demuestra en azul y la línea de la tangente está en rojo). Vemos que x_{n + 1} es una aproximación mejor que x_n para la raíz x de la función f.

En la ilustración adjunta del método de Newton se puede ver que x_{n + 1} es una mejor aproximación que x_n para el cero (x) de la función f.

Una forma alternativa de obtener el algoritmo es desarrollando la función f (x) en serie de Taylor, para un entorno del punto x_n:

Si se trunca el desarrollo a partir del término de grado 2, y evaluamos en x_{n + 1}:

Si además se acepta que x_{n + 1} tiende a la raíz, se ha de cumplir que f(x_{n + 1}) = 0, luego, sustituyendo en la expresión anterior, obtenemos el algoritmo.

Finalmente, hay que indicar que el método de Newton-Raphson puede interpretarse como un método de iteración de punto fijo. Así, dada la ecuación f(x) = 0, se puede considerar el siguiente método de iteración de punto fijo:

Se escoge h (x) de manera que g'(r)=0 (r es la raíz buscada). Dado que g'(r) es:

Entonces:

Como h (x) no tiene que ser única, se escoge de la forma más sencilla:

Por tanto, imponiendo subíndices:

Expresión que coincide con la del algoritmo de Newton-Raphson

Convergencia del Método

El orden de convergencia de este método es, por lo menos, cuadrático. Sin embargo, si la raíz buscada es de multiplicidad algebraica mayor a uno (i.e, una raíz doble, triple, ...), el método de Newton-Raphson pierde su convergencia cuadrática y pasa a ser lineal de constante asintótica de convergencia 1-1/m, con m la multiplicidad de la raíz.

Existen numerosas formas de evitar este problema, como pudieran ser los métodos de aceleración de la convergencia tipo Δ² de Aitken o el método de Steffensen. Derivados de Newton-Raphson destacan el método de Ralston-Rabinowitz, que restaura la convergencia cuadrática sin más que modificar el algoritmo a:

Evidentemente, este método exige conocer de antemano la multiplicidad de la raíz, lo cual no siempre es posible. Por ello también se puede modificar el algoritmo tomando una función auxiliar g(x) = f(x)/f'(x), resultando:

Su principal desventaja en este caso sería lo costoso que pudiera ser hallar g(x) y g'(x) si f(x) no es fácilmente derivable.

Por otro lado, la convergencia del método se demuestra cuadrática para el caso más habitual en base a tratar el método como uno de punto fijo: si g'(r)=0, y g' '(r) es distinto de 0, entonces la convergencia es cuadrática. Sin embargo, está sujeto a las particularidades de estos métodos.

Nótese de todas formas que el método de Newton-Raphson es un método abierto: la convergencia no está garantizada por un teorema de convergencia global como podría estarlo en los métodos de falsa posición o de bisección. Así, es necesario partir de una aproximación inicial próxima a la raíz buscada para que el método converja y cumpla el teorema de convergencia local.

Estimación del Error

Se puede demostrar que el método de Newton-Raphson tiene convergencia cuadrática: si α es raíz, entonces:

para una cierta constante C. Esto significa que si en algún momento el error es menor o igual a 0,1, a cada nueva iteración doblamos (aproximadamente) el número de decimales exactos. En la práctica puede servir para hacer una estimación aproximada del error:

Error relativo entre dos aproximaciones sucesivas:

Con lo cual se toma el error relativo como si la última aproximación fuera el valor exacto. Se detiene el proceso iterativo cuando este error relativo es aproximadamente menor que una cantidad fijada previamente.

Teorema de Convergencia Local del Método de Newton

Sea . Si , y , entonces existe un r>0 tal que si , entonces la sucesión x_n con verifica que:

para todo n y x_n tiende a p cuando n tiende a infinito.

Si además , entonces la convergencia es cuadrática.

Ejemplo

Consideremos el problema de encontrar un número positivo x tal que cos(x) = x³. Podríamos tratar de encontrar el cero de f(x) = cos(x) - x³.

Sabemos que f '(x) = -sin(x) - 3x². Ya que cos(x) ≤ 1 para todo x y x³ > 1 para x>1, deducimos que nuestro cero está entre 0 y 1. Comenzaremos probando con el valor inicial x₀ = 0,5

Los dígitos correctos están subrayados. En particular, x₆ es correcto para el número de decimales pedidos. Podemos ver que el número de dígitos correctos después de la coma se incrementa desde 2 (para x₃) a 5 y 10, ilustando la convergencia cuadrática.

En pseudocódigo, esto es:

function newtonIterationFunction(x) {
    return  x - (cos(x) - x^3) / (-sin(x) - 3*x^2)     
}
 
var x := 0,5
 
for i from 0 to 99 {
    print "Iteraciones: " + i
    print "Valor aproximado: " + x
    xold := x
    x := newtonIterationFunction(x) 
    if x = xold {
        print "Solución encontrada!"
        break
    }
}

Codigo en MatLab

Programa escrito en Matlab para hallar las raíces usando el método de NEWTON-RAPHSON

function x =newton()
disp ('NEWTON-RAPHSON')
xo=input('Valor inicial =');
n=input ('numero de iteraciones=');
salida=ones(n,4); % matiz de salida de datos 
for i=1:n
    x1=xo-[(exp(-xo)-xo)]/[(-exp(-xo)-1)];
    vsal=[xo;x1];
    er=[[abs((xo-x1)/xo)]]*100;  % error relativo porcentual 
    ea=[[abs((x1-xo)/x1)]]*100;  % error 
    xo=x1;
 
    salida(i,1)=i;
    salida(i,2)=x1;
    salida(i,3)=er;
    salida(i,4)=ea;
end
disp('ite raiz er ea');
disp(num2str(salida));

El programa siguiente hace el cálculo para una superficie.

syms x1
syms x2
syms x3
V=['sin(x1)+2^x2+log(x3)-7';'3*x1+2*x2-x3^3+1      ';'x1+x2+x3-5            '];
%se calcula el jacobiano:
DV(1,:)=[diff(V(1,:),x1), diff(V(1,:),x2),diff(V(1,:),x3)];
DV(2,:)=[diff(V(2,:),x1), diff(V(2,:),x2),diff(V(2,:),x3)];
DV(3,:)=[diff(V(3,:),x1), diff(V(3,:),x2),diff(V(3,:),x3)];
%se da el valor de partida:
x1=0;
x2=4;
x3=2;
x_1o=[x1;x2;x3];
%se calcula H en ese punto
Vo(1,:)=eval(V(1,:));
Vo(2,:)=eval(V(2,:));
Vo(3,:)=eval(V(3,:));
%Se calcula el Hessiano en ese punto
DV1=eval(DV);
%se calcula la Inversa del Hessiano en ese punto
DV_1=DV1^-1;
%se calcula el siguiente valor de iteración
x_1=[x1;x2;x3]-DV_1*Vo;
%cantidad de iteraciones maxima:
n=50; 
%se define a = n, si se cumple condicion de error antes,  cambia
a=n; 
 
for i=1:n  
%error relativo entre aproximaciones sucecivas
    er=norm(x_1-x_1o)/norm(x_1);
    if er<.0001
        a=i;
       'break;' end
 
    x1=x_1(1);
    x2=x_1(2);
    x3=x_1(3);
    x_1o=[x1;x2;x3];
    Vo(1,:)=eval(V(1,:));
    Vo(2,:)=eval(V(2,:));
    Vo(3,:)=eval(V(3,:));
    DV1=eval(DV);
    DV_1=DV1^-1;
    x_1=[x1;x2;x3]-DV_1*Vo;  
 
end
    a
    x_1

Referencias

• Tjalling J. Ypma, Historical development of the Newton-Raphson method, SIAM Review 37 (4), 531–551, 1995.
• P. Deuflhard, Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms. Springer Series in Computational Mathematics, Vol. 35. Springer, Berlin, 2004. ISBN 3-540-21099-7.
• C. T. Kelley, Solving Nonlinear Equations with Newton's Method, no 1 in Fundamentals of Algorithms, SIAM, 2003. ISBN 0-89871-546-6.
• J. M. Ortega, W. C. Rheinboldt, Iterative Solution of Nonlinear Equations in Several Variables. Classics in Applied Mathematics, SIAM, 2000. ISBN 0-89871-461-3.
• W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, 1992. ISBN 0-521-43108-5 (available free online, with code samples: [1]), sections 9.4 [2] and 9.6 [3].
• W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling, Numerical Recipes: The Art of Scientific Computing, Cambridge University Press, 2007. ISBN 0-521-88068-8 (available for a fee online, with code samples [4]).
• W. H. Press, B. P. Flannery, S. A. Teukolsky, W. T. Vetterling, Numerical Recipes in Fortran, Cambridge University Press, 1992. ISBN 0-521-43064-X (online, with code samples: [5])
• Endre Süli and David Mayers, An Introduction to Numerical Analysis, Cambridge University Press, 2003. ISBN 0-521-00794-1.
• Weisstein, Eric W. «Newton's method and Convergence» (en inglés). MathWorld. Wolfram Research. Consultado el 29 de agosto de 2009.

Enlaces externos

• Método de Newton aplicado al cálculo de la raíz cuadrada de un número
• El método de Newton en Mathcad Application Server (con animación)
• Método de Newton-Raphson: Notas, PPT, Mathcad, Maple, Matlab, Mathematica