Teorema de De Gua

El teorema de De Gua, llamado así en honor al matemático francés Jean Paul de Gua de Malves, es un análogo en tres dimensiones del teorema de Pitágoras. Este teorema establece que si un tetraedro posee un vértice formado por ángulos rectos (como en el caso de los vértices de un cubo), entonces el cuadrado del área de la cara opuesta a dicho vértice es igual a la suma de los cuadrados de las áreas de las otras tres caras. A partir de las figuras:

Vista frontal: cara opuesta al vértice.	Vista trasera: caras que forman los ángulos rectos del vértice	Vista lateral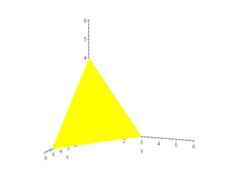

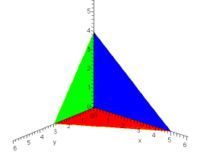
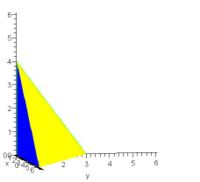
El teorema de Pitágoras y el teorema de De Gua son casos especiales (para un número de dimensiones n = 2 y n = 3 respectivamente) de un teorema general para un símplex que posea un vértice con un ángulo recto.

Referencias

• Este artículo fue creado a partir de la traducción del artículo De Gua's theorem de la Wikipedia en inglés, concretamente de esta versión, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.
• Alvarez, Sergio A. «Note on an n-dimensional Pythagorean theorem», Universidad Carnegie Mellon (en inglés).
• GoGeometry from the Land of the Incas (2007), «De Gua's Theorem, Pythagorean theorem in 3-D» (en inglés). Consultado el 6 de junio de 2010.
• Weisstein, Eric W. «de Gua's Theorem» (en inglés). MathWorld. Wolfram Research. Consultado el 6 de junio de 2010.