- Bifurcación (matemática)
-
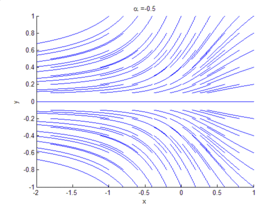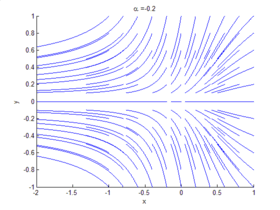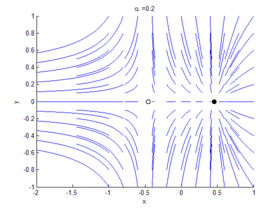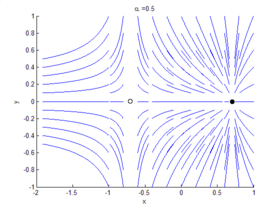
La Teoría de bifurcaciones es un campo matemático centrado en el estudio de los cambios en la estructura cualitativa o topológica de una familia determinada. Ejemplos de tales familias son las curvas integrales de un campo vectorial, y las soluciones de una familia de ecuaciones diferenciales. Generalmente en referencia a sistemas dinámicos, una bifurcación se da cuando una pequeña variación en los valores de los parámetros de un sistema (parámetros de bifurcación) causa un brusco cambio "cualitativo" o topológico en su comportamiento.[1] Las bifurcaciones pueden producirse tanto en sistemas continuos como en sistemas discretos.
Contenido
Tipos de bifurcaciones
Bifurcaciones locales
Retrato de fase que muestra una bifurcación fold.
Las bifurcaciones locales son aquellas que pueden ser analizadas completamente mediante cambios en las propiedades de la estabilidad local —bien sean éstas de puntos de equilibrio, órbitas locales u otros conjuntos invariantes— conforme los parámetros atraviesan umbrales críticos.
Las bifurcaciones locales más típicas son:
- Bifurcación tangencial o fold
- Bifurcación de Pitchfork
- Bifurcación transcrítica
- Bifurcación de Hopf
Bifurcaciones globales
Las bifurcaciones globales ocurren normalmente en mayores conjuntos invariantes del sistema, los cuales "colisionan" entre ellos o con los puntos de equilibrio del sistema. Por tanto, no pueden ser detectados de forma exclusiva mediante un análisis de los puntos de equilibrio.
Las bifurcaciones globales más típicas son:
- Bifurcación homoclínica
- Bifurcación heteroclínica
- Bifurcación de período infinito
Véase también
- Diagrama de bifurcación
Referencias
- ↑ P. Blanchard, R.L. Devaney, G.R. Hall, Differential Equations, Thompson, 2006, pp. 96-111
Enlaces externos
- (en inglés) Sistemas dinámicos no lineales
Categoría:- Sistemas dinámicos
Wikimedia foundation. 2010.
