- Triángulo de Kepler
-
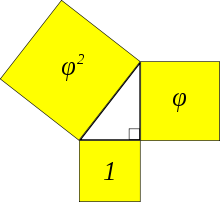fig. tk1: El triángulo de Kepler es un triángulo rectángulo formado por tres cuadrados con áreas en progresión geométrica de acuerdo al número áureo.
El triángulo de Kepler es un triángulo rectángulo con lados en progresión geométrica. La relación entre lados de un triángulo de Kepler, está vinculada al número áureo.[1] [2]
y puede ser escrita:
, o aproximadamente 1 : 1,272 : 1,618.[3] Los cuadrados de los lados de éste triángulo (véase fig. tk1) están en progresión geométrica de acuerdo al número áureo.Los triángulos con dicha relación son llamados triángulos de Kepler, dado que el matemático y astrónomo alemán Johannes Kepler (1571–1630) fue el primero en demostrar que este triángulo se caracteriza por tener una relación entre los catetos y la hipotenusa igual a la proporción áurea.[4] El triángulo de Kepler combina dos conceptos clave de la matemática, el teorema de Pitágoras y número áureo, lo cual fascinó profundamente a Kepler, como quedó expresado en su propia cita:
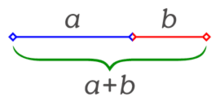fig.me1: Una sección áurea[1] es una división en dos partes de un segmento, según las proporciones[2] dadas por el número áureo
. La longitud total a + b es al segmento más largo a, como a es al segmento más corto b.La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras, el otro la división de un segmento entre el extremo y su proporcional.[1] Al primero lo podemos comparar a un montón de oro, al segundo lo podemos llamar una piedra preciosa.[5]
traducción de cita de Johannes KeplerPara una aclaración del significado de “la división de un segmento entre el extremo y su proporcional”,[1] ver fig.me1.
Contenido
Deducción
El hecho de que un triángulo de lados 1,
y φ sea rectángulo, se deduce con solo reescribir el polinomio cuadrático de definición del número áureo φ:[2]
en la forma del teorema de Pitágoras:
Relación con las medias aritmética, geométrica, y armónica
Para números reales positivos a y b, sus media aritmética, media geométrica y media armónica, son las longitudes de los lados de un triángulo rectángulo, si y solo si tal triángulo es un triángulo de Kepler.[6]
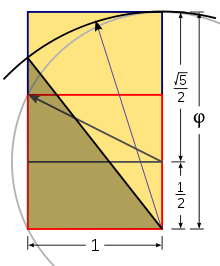
Cómo construir un triángulo de Kepler
fig.ct1: Método para construir un triángulo de Kepler mediante la proporción áurea.Un triángulo de Kepler puede ser construido usando solo regla y compás creando primero un rectángulo áureo:
- Construir un simple cuadrado, (rojo en fig.ct1).
- Trazar una línea desde el punto medio de uno de sus lados hasta un vértice del lado opuesto.
- Utilizar la longitud de esa línea, como radio para dibujar un arco (gris en la figura) que define la altura de un rectángulo áureo.
- Completar el dibujo de dicho rectángulo.
- Úsese el lado largo de la derecha del rectángulo, para trazar un arco hasta que intercepte al lado opuesto del rectángulo, dicha intersección define las longitudes de la hipotenusa y del cateto mayor del triángulo de Kepler (área marrón en fig.ct1).
Kepler lo construía de manera diferente. Según una carta que le escribió a su antiguo profesor Michael Mästlin:[4] "Si un segmento se divide entre el extremo y su proporcional,[1] y se toma como hipotenusa de un triángulo rectángulo cuyo ángulo recto se halle sobre el punto que divide a la hipotenusa en dichas partes, entonces el cateto menor tendrá la misma longitud que la parte más larga del segmento de partida (ahora hipotenusa)."[7]
Curiosidades
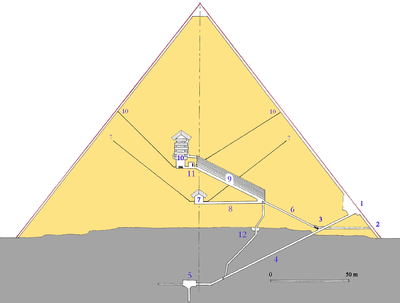
Algunas fuentes afirman que se puede reconocer en la gran pirámide de Guiza un triángulo con dimensiones aproximadas a un triángulo de Kepler.[8] [9]
El corte de la pirámide de Keops es muy aproximada a dos triángulos de Kepler enfrentados.Véase también
Notas y referencias
- ↑ a b c d e Euclides en Los Elementos: "Se dice que una línea recta está dividida entre el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor."
- ↑ a b c Al resolver la ecuación de segundo grado de la definición del número áureo
se obtiene su valor numérico 
. - ↑ Roger Herz-Fischler (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0889203245. http://books.google.com/books?id=066T3YLuhA0C&pg=PA81&dq=kepler-triangle+geometric&ei=ux77Ro6sGKjA7gLzrdjlDQ&sig=bngzcQrK9nHOkfZTo5O0ieNdtUs.
- ↑ a b Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. pp. 149. ISBN 0-7679-0815-5.
- ↑ Karl Fink, Wooster Woodruff Beman, and David Eugene Smith (1903). A Brief History of Mathematics: An Authorized Translation of Dr. Karl Fink's Geschichte der Elementar-Mathematik (2nd ed. edición). Chicago: Open Court Publishing Co. http://books.google.com/books?id=3hkPAAAAIAAJ&pg=PA223&dq=%22Geometry+has+two+great+treasures%22&lr=&as_brr=1&ei=sQ1GSI_KH4fstgO_rvCpDQ.
- ↑ Di Domenico, Angelo, "The golden ratio—the right triangle—and the arithmetic, geometric, and harmonic means," The Mathematical Gazette 89, 2005.
- ↑ Pasaje de carta de Kepler, traducido del inglés, con licencias didácticas.
- ↑ The Best of Astraea: 17 Articles on Science, History and Philosophy. Astrea Web Radio. 2006. ISBN 1425970400. http://books.google.com/books?id=LDTPvbXLxgQC&pg=PA93&dq=kepler-triangle&ei=vCH7RuG7O4H87gLJ56XlDQ&sig=6n43Hhu5pE3TN5BW18tbQJGRHTQ.
- ↑ Squaring the circle, Paul Calter
Categoría:- Triángulos
Wikimedia foundation. 2010.
