Triángulo rectángulo

Un triángulo rectángulo y sus elementos.

Triángulo rectángulo se denomina al triángulo en el que uno de sus ángulos es recto, es decir, mide 90° (grados sexagesimales) ó π/2 radianes.

(Clasificación por amplitud de sus ángulos)

Triángulos

Rectángulos

Oblicuángulos

Obtusángulos

Acutángulos

Fórmulas para calcular un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.

**Pitágoras ( c²=a²+b² ) – Fórmulas prácticas**
$a = +\sqrt {c^2 - b^2}$	$b= +\sqrt{c^2-a^2}$	$c = +\sqrt {a^2 + b^2}$

Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto.

Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.

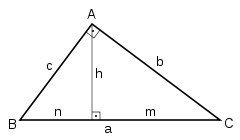
Cualquier triángulo se puede dividir en 2 triángulos rectángulos.

Contenido

1 Nombre de sus elementos (designación convencional)
2 Relaciones métricas
3 Razones trigonométricas
4 Área
5 Notas
6 Véase también
7 Enlaces externos

Nombre de sus elementos (designación convencional)

Los elementos principales de un triángulo rectángulo son: vértices, lados y ángulos.
Para la designación convencional de los mismos véase → ( ^[1] )

Relaciones métricas

En un triángulo rectángulo:

La medida de un cateto es media proporcional entre la medida de la hipotenusa y su proyección sobre ella.

$\frac{a}{b} = \frac{b}{m}$ , también se cumple: $\frac{a}{c} = \frac{c}{n}$

La medida de la altura es media proporcional entre los dos segmentos que determina sobre la hipotenusa.

$\frac{m}{h} = \frac{h}{n}$ , es decir: $h^2 = m \cdot n \,$

Las tres alturas del triángulo rectángulo pueden calculase como:

$h_a=\frac{b\cdot c}{a}$ ; $h b = c$ ; $h c = b$

donde b y c son los catetos y a, la hipotenusa, en tanto que h_a, h_b y h_c son las alturas sobre los respectivos lados.

La relación entre catetos e hipotenusa se establece mediante el Teorema de Pitágoras:

$a^2 = b^2 + c^2 \,$

donde $a \,$ es la medida de la hipotenusa.

Razones trigonométricas

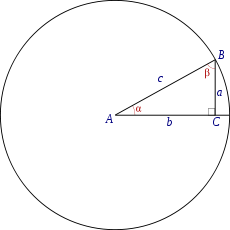
En un triángulo rectángulo, las razones trigonométricas del ángulo $\alpha \;$ con vértice en A, son:

El seno: la razón entre el cateto opuesto y la hipotenusa,

$\text{sen}(\alpha)= \frac{a}{c}$

El coseno: la razón entre el cateto adyacente y la hipotenusa,

$\cos(\alpha)= \frac{b}{c}$

La tangente: la razón entre el cateto opuesto y el adyacente,

$\tan(\alpha)= \frac{a}{b}$

Área

fig. ar1: Relación entre el rectángulo y dos de las tres alturas (la de los catetos) de un triángulo rectángulo.

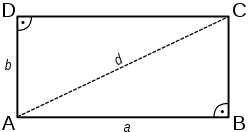
Se puede considerar el área de un triángulo rectángulo como la mitad del área de un rectángulo partido por su diagonal, véase fig. ar1, (o un cuadrado si el triángulo rectángulo es además isósceles).

(A1) $A = \frac{b \cdot a}{2}$

donde a y b de la ecuación (A1) representan las medidas de los dos catetos que coinciden con los dos lados y las correspondientes alturas del rectángulo (véase fig. ar1).

En todo triángulo rectángulo cada uno de los dos catetos es siempre la respectiva altura del otro. Asumiendo que a = cateto1 y b = cateto2 se puede escribir una versión equivalente de ecuación (A1) de la siguiente manera:

$A = \frac{cateto1 \cdot cateto2}{2}$

La demostración anterior es solo un caso especial, restringido, de una mucho más general que vale para todo triángulo (no solo para los triángulos rectángulos); Y esta es la "proposición I.41^[2] de Euclides, la cual se basa en el concepto más general de paralelogramo y no se restringe al rectángulo. Dicha proposición I.41 extiende la validez de la ecuación (A1) a todo triángulo.

Notas

↑
Triángulos — Resumen de convenciones de designación
Vértices $A$ $B$ $C$

Lados (como segmento) $BC$ $AC$ $AB$

Lados (como longitud) $a$ $b$ $c$

Ángulos $\widehat{\alpha} = \widehat{a} = \widehat{A} = \widehat{BAC}$ $\widehat{\beta} = \widehat{b} = \widehat{B} = \widehat{ABC}$ $\widehat{\gamma} = \widehat{c} = \widehat{C} = \widehat{ACB}$
↑ Euclides Los Elementos, proposición I.41 → "Si un paralelogramo tiene la misma base que un triángulo y está contenido entre las mismas paralelas, el paralelogramo es el doble del triángulo".

**Triángulos — Resumen de convenciones de designación**
Vértices	$A$	$B$	$C$
*Lados (como segmento)*	$BC$	$AC$	$AB$
*Lados (como longitud)*	$a$	$b$	$c$
Ángulos	$\widehat{\alpha} = \widehat{a} = \widehat{A} = \widehat{BAC}$	$\widehat{\beta} = \widehat{b} = \widehat{B} = \widehat{ABC}$	$\widehat{\gamma} = \widehat{c} = \widehat{C} = \widehat{ACB}$

Véase también

Enlaces externos

Wikimedia Commons alberga contenido multimedia sobre Triángulo rectángulo. Commons
Weisstein, Eric W. «Triángulo rectángulo» (en inglés). MathWorld. Wolfram Research.

Categoría:

Triángulos

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

Triángulo rectángulo — Un triángulo rectángulo es un triángulo en el que uno de sus tres ángulos es recto, es decir, mide 90º o p/2 radianes. Este tipo de triángulo cumple el Teorema de Pitágoras. Como muestra la figura adjunta, la hipotenusa es el lado opuesto al… … Enciclopedia Universal
triángulo rectángulo u ortogonio — ► locución GEOMETRÍA El que tiene uno de sus ángulos recto … Enciclopedia Universal
Triángulo sagrado egipcio — o Triángulo egipcio,[1] es el nombre moderno dado a un triángulo rectángulo cuyo lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para… … Wikipedia Español
triángulo — (Del lat. triangŭlus). 1. adj. De forma de triángulo. 2. m. Polígono de tres lados. 3. Mús. Instrumento que consiste en una varilla metálica doblada en forma triangular y suspendida de un cordón, la cual se hace sonar golpeándola con otra varilla … Diccionario de la lengua española
rectángulo — rectángulo, la (Del lat. rectangŭlus). 1. adj. Geom. Dicho principalmente del triángulo o del paralelepípedo: Que tiene ángulos rectos. 2. m. Geom. Paralelogramo que tiene los cuatro ángulos rectos y los lados contiguos desiguales. ☛ V. triángulo … Diccionario de la lengua española
rectángulo — adjetivo 1. [Figura geométrica] que tiene ángulos rectos. triángulo rectángulo Triángulo que tiene un ángulo recto. sustantivo masculino 1. Figura geométrica de cuatro lados, que tiene los ángulos rectos y los lados iguales dos a dos: El… … Diccionario Salamanca de la Lengua Española
Triángulo — Para otros usos de este término, véase Triángulo (desambiguación). El triángulo es un polígono de tres lados. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran… … Wikipedia Español
Triángulo de Kepler — fig. tk1: El triángulo de Kepler es un triángulo rectángulo formado por tres cuadrados con áreas en progresión geométrica de acuerdo al número áureo. El triángulo de Kepler es un triángulo rectángulo con lados en progresión geométrica. La… … Wikipedia Español
Triángulo — ► adjetivo 1 Que tiene la forma de un polígono de tres lados. ► sustantivo masculino 2 GEOMETRÍA Polígono de tres lados que se cortan formando tres ángulos. 3 MÚSICA Instrumento de percusión formado por una varilla metálica con la forma de ese… … Enciclopedia Universal
Rectángulo — ► adjetivo 1 GEOMETRÍA Se aplica a la figura, en especial al triángulo o al paralelepípedo, que tiene ángulos rectos. ► sustantivo masculino 2 GEOMETRÍA Cuadrilátero que tiene los cuatro ángulos rectos y los lados iguales dos a dos. * * *… … Enciclopedia Universal

Los diccionarios y las enciclopedias sobre el Académico

Triángulo rectángulo

Contenido

Nombre de sus elementos (designación convencional)

Relaciones métricas

Razones trigonométricas

Área

Notas

Véase también

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Triángulo rectángulo

Contenido

Nombre de sus elementos (designación convencional)

Relaciones métricas

Razones trigonométricas

Área

Notas

Véase también

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo