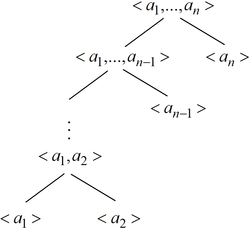Álgebra de las palabras

El álgebra de las palabras estudia la formalización gramatical de las construcciones de palabras sobre un alfabeto para un lenguaje, desde una perspectiva matemática que nos permita, de un modo firme, afirmar o rechazar diversos resultados necesarios para fundamentar cualquier modelo matemático de un lenguaje, y más inmediatamente el lenguaje proposicional.

Contenido

1 El álgebra de las palabras sobre un alfabeto

Los alfabetos se asociaran a conjuntos que pueden ser finitos, numerables o mejor simplemente infinitos de símbolos.

Introducción

La notación utilizada es la desarrollada en teoría de conjuntos, por lo que requiere una base mínima para un rápido trabajo y asimilación con simplicidad y fluidez de los nuevos conceptos.

Para introducir nociones que nos permitan unir símbolos necesitamos las siguientes definiciones.

Par ordenado

Dado un par de elementos de un conjunto $A_{}^{}$ , es decir, $a,b \in A$ , llamaremos a $<a,b>_{}^{}$ un par ordenado.

Nota: estos pares pueden ser formalmente elementos de nuevos conjuntos sin ningún impedimento, y se puede comparar con otros pares ordenados $<c,d>_{}^{}$ exclusivamente en este orden, primero a con c y luego b con d.

Producto cartesiano

Llamaremos producto cartesiano de dos conjuntos $A_{}^{}$ y $B_{}^{}$ al conjunto $A \times B := \{ <a ,\; b> : a \in A ,\; b \in B \}.$

Palabras sobre un alfabeto

Dado un conjunto $A_{}^{}$ y un número natural $n \geq 1_{}^{}$ , definiremos el conjunto de las sucesiones finitas de longitud n de elementos de $A_{}^{}$ , $A_{}^n$ , como el n-ésimo conjunto de la lista siguiente definida por inducción:

$\begin{matrix} A^1 & = & A \\ A^2 & = & A \times A \\ & \vdots & \\ A^n & = & A^{n-1} \times A \\ & \vdots & \end{matrix}$

Llamaremos palabras sobre un alfabeto $A_{}^{}$ al conjunto de las sucesiones finitas de elementos de A definido como el conjunto $A^{\ast} = \bigcup_{n \geq 1} A^n$ , es decir, las palabras son por definición una colección de todas las sucesiones finitas de elementos de un mismo alfabeto.

Notaciones

Los elementos de $A^1_{}$ son elementos notados por $x := < x_{}^{}>$ donde $x \in A.$

Los elementos de $A^2_{}$ son pares ordenados, notados como $< a ,\; b >:=<<a> ,\; b_{}^{}>$ donde $a,b \in A.$

Los elementos de $A^3_{}$ son ternas ordenadas, notadas como $< a ,\; b ,\; c >:=<<a ,\; b >,\; c_{}^{} >$ donde $a,b,c \in A.$

En general, para $A^n_{}$ tenemos sucesiones finitas de longitud n notadas como $< a_1 ,\; \dots ,\; a_{n-1}^{} ,\; a_n >:=$ $< < a_1 ,\; \dots ,\; a_{n-1}^{} > ,\; a_n >$ donde $a_i \in A$ , $\forall i \in \{1 ,\; \dots ,\; n \}.$

Para determinar el contenido de un elemento $a \in A^n_{}$ se indica como $a=<a_1 ,\; \dots ,\; a_n^{}>$ donde $a_i^{}$ será el i-ésimo termino de la sucesión.

Esta última notación nos permite, ya, comparar palabras, veamos los resultados siguientes:

Sucesiones de igual longitud

Dado dos elementos $a^n,b^n \in A^n$ , entonces

$a^n=<a_1 ,\; \dots ,\; a_n > = <b_1^{} ,\; \dots ,\; b_n >=b^n \Leftrightarrow$ $a_i=b_i ,\; \forall i \in \{1 ,\; \dots ,\; n \}.$

No es necesario definirlo así, pues se puede demostrar a partir de las definiciones que ya tenemos, la demostración habitual, para sucesiones, es comparando los elementos ordenadamente según existan, es decir, mediante inducción:

Si n=1, tenemos $<a_1^{}>=<b_1>$ por notación sabemos que $a_1^{}=b_1.$

Si n=2, es decir un par ordenado, tenemos $<a_1 ,\; a_2>=<b_1 ,\; b_2^{}>$ por comparación de un par ordenado $a_1=b_1^{}$ y $a_2=b_2^{}.$

Supongamos que para el caso n-1 es cierto, veamos ahora que también lo es para n, es decir, que es cierto que $a^{n-1}=<a_1 ,\; \dots ,\; a_{n-1}^{}> =$ $<b_1 ,\; \dots ,\; b_{n-1}^{} >=b^{n-1} \Leftrightarrow$ $a_i=b_i ,\; \forall i \in \{1 ,\; \dots ,\; n-1 \}$ , y ahora tenemos que comprobarlo para el caso n:

$<<a_1 ,\; \dots ,\; a_{n-1} > ,\; a_n^{} >=<<b_1 ,\; \dots ,\; b_{n-1} > ,\; b_n >$ , es decir, $<<a^{n-1}> ,\; a_n >=<<b^{n-1}> ,\; b_n^{}>$ , es decir, $< a^{n-1} ,\; a_n >=<b^{n-1} ,\; b_n^{}> \Leftrightarrow$ $a^{n-1}=b_{}^{n-1}$ y $a_n=b_n^{}$ como vimos en el caso n=2.

Sucesiones de diferente longitud

Dado dos elementos $a^m,b^{m+k} \in A^\ast$ tales que $a_{}^m=$ $<a_1 ,\; \dots ,\; a_m^{} >=$ $<b_1^{} ,\; \dots ,\; b_{m+k}>=$ $b_{}^{m+k}$ con k>0 y m>1, entonces:

$a_1^{}=<b_1 ,\; \dots ,\; b_{k+1}^{}>$ y $a_i=b_{i+k}^{}$ , $\forall i \in \{1 ,\; \dots ,\; m \}.$

Informalmente es evidente que $a_1^{}=$ $<b_1 ,\; \dots ,\; b_{k+1}^{}>$ debido al resultado anterior para sucesiones de igual longitud, para demostrarlo formalmente se procede del modo siguiente:

Si m=1, tenemos directamente que $a_1^{}=$ $<b_1 ,\; \dots ,\; b_{k+1}^{}>$ , y por tanto es cierto.

Si m=2, tenemos que $<a_1^{} ,\; a_2>=$ $<<b_1 ,\; \dots ,\; b_{k+1}> ,\; b_{k+2}>$ , como par ordenado, sucede que $a_1^{}=$ $<b_1 ,\; \dots ,\; b_{k+1}^{}>.$

Supongamos que para el caso m-1 es cierto, veamos ahora que también lo es para m:

Por hipótesis podemos tomar el par ordenado $<<a_1 ,\; \dots ,\; a_{m-1}^{}> ,\; a_m>=$ $<<b_1 ,\; \dots ,\; b_{(m-1)+k}> ,\; b_{m+k}^{}>$ , esto prueba la certeza, pues tienen las mismas hipótesis para una k>0 fijada.

Corolario

Dado un conjunto $A_{}^{}$ sin elementos expresados mediante sucesiones finitas de sus propios elementos, si $a,b \in A_{}^\ast : a=b$ entonces:

a y b son de la misma longitud,

$A_{}^n \cap A^m = \emptyset$ para $n \neq m_{}^{}.$

Concatenación

Llamaremos operación concatenación entre sucesiones finitas a:

$\begin{matrix} \circ : & A^\ast \times A^\ast & \longrightarrow & A^\ast \\ & < <a_1 ,\; \dots ,\; a_n>,<b_1 ,\; \dots ,\; b_m> > & \longmapsto & <a_1 ,\; \dots ,\; a_n > \circ <b_1 ,\; \dots ,\; b_m> = <a_1 ,\; \dots ,\; a_n ,\; b_1 ,\; \dots ,\; b_m>. \end{matrix}$

Por tanto la estructura $<A^\ast ,\; \circ >$ es un grupoide libre generado por el conjunto $A_{}^{}$ .

Para referirnos al mismo objeto matemático, escribiremos por comodidad simplemente $a_1 \dots a_n :=$ $<a_1 ,\; \dots ,\; a_n>=$ $<a_1>\circ \cdots \circ<a_n>.$

Páginas relacionadas

lenguaje proposicional

lenguaje de orden cero

lenguaje de predicados

lenguaje de primer orden

Bibliografía

Herbert B. Enderton, Elements of set theory, Academic Press, INC. 1977.

Contiene normas para la correcta lectura del texto.

Herbert B. Enderton, A mathematical introduction to logic, A Harcourt Science an Tecnology Company 2001.

Exposición propia del álgebra de las palabras.

Nino B. Cocchiarella and Max A. Freund, Modal Lógica An Introduction to Its Syntax and Semantics, Oxford 2008.

Contiene un resumen en el primer tema con cierta informalidad.

Categoría:

Lógica formal

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

Teorema fundamental del álgebra — El teorema fundamental del álgebra establece que un polinomio en una variable, no constante y con coeficientes complejos, tiene tantas raíces[1] como indica su grado, contando las raíces con sus multiplicidades. En otras palabras, dado un… … Wikipedia Español
Invariante algebraico (álgebra lineal) — Un invariante algebraico es una función polinómica de las componentes de la matriz de una aplicación lineal, no depende de la base vectorial escogida para representar la aplicación lineal en forma de matriz. En otras palabras, un invariante… … Wikipedia Español
Objeto libre — En las Matemáticas, uno de los conceptos fundamentales del álgebra abstracta es la idea del objeto libre. Forma parte del álgebra universal, puesto que se relaciona a todos los tipos de estructura algebraica (con operaciones finitas). También se… … Wikipedia Español
Lógica empírica — La lógica empírica es la base del razonamiento empírico y por lo tanto del método empírico. Esta visión de la lógica proviene de la antigua Grecia. El término empírico deriva del griego antiguo de experiencia, έμπειρία, que a su vez deriva de έυ… … Wikipedia Español
Al-Juarismi — Sello emitido el 6 de septiembre de 1983 en la Unión Soviética conmemorando el aniversario n.º 1200 (aproximado) del matemático árabe. Abu Abdallah Muḥammad ibn Mūsā al Jwārizmī (Abu Yāffar) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر),… … Wikipedia Español
Matemática en el islam medieval — Tratado de arte numeral de Joannis de Sacro Bosco. La matemática árabe se enriqueció en forma creciente a medida que los musulmanes conquistaron territorios. Con rapidez inusitada, el islamismo se expandió en todo el territorio que se extiende… … Wikipedia Español
Matemática en el Islam medieval — Saltar a navegación, búsqueda Contenido 1 Valoración de la ciencia islámica 2 Desarrollos y contexto histórico 3 Otros ejemplos de desarrollo … Wikipedia Español
Maude — Este artículo o sección sobre informática necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 10 de septiembre de 2008. También… … Wikipedia Español
Ayuda:Cómo se edita una página — Ayuda de edición Antes de comenzar La interfaz de Wikipedia Barra de herramientas de edición Cómo se edita una página Creando un artículo Cómo empezarlo Cómo cambiarle el título (1) (2) Manual de estilo … Wikipedia Español
Gramática del español — Estatua del gramático Antonio de Nebrija en la Biblioteca Nacional de Madrid, por Anselmo Nogués. En 1492, Nebrija fue el primer europeo en escribir una gramática de una lengua románica o neolatina, el español … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Álgebra de las palabras

Contenido