Secuencia de Prüfer

En matemática combinatoria, la secuencia de Prüfer (o código de Prüfer) de un árbol etiquetado es una secuencia única asociada al árbol. La secuencia de un árbol con n vértices tiene longitud n − 2, y puede ser generada por un algoritmo iterativo simple. Las secuencias de Prüfer fueron usadas por primera vez por Heinz Prüfer para probar la fórmula de Cayley en 1918.^[1]

Algoritmo para convertir un árbol en una secuencia de Prüfer

La secuencia de Prüfer de un árbol etiquetado se puede generar removiendo iterativamente los vértices del árbol hasta que queden solamente dos vértices. Específicamente, consideremos un árbol etiquetado T con vértices {1, 2, ..., n}. En el paso i, remover la hoja con la menor etiqueta y hacer que el i-ésimo elemento de la secuencia de Prüfer sea la etiqueta del nodo vecino de la hoja removida.

La secuencia del árbol etiquetado es claramente única y tiene longitud n − 2.

Ejemplo

Un árbol etiquetado con secuencia de Prüfer 4445.

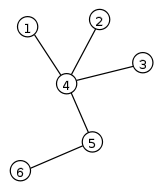
Consideremos la ejecución del algoritmo descrito anteriormente sobre el ejemplo mostrado a la derecha. Inicialmente, el vértice 1 es la hoja con la menor etiqueta, luego es la primera en ser removida y se anota un "4" en la secuencia de Prüfer. Los vértices 2 y 3 son removidos a continuación, luego se agrega un "4" dos veces más. El vértice 4 es ahora una hoja y tiene la etiqueta menor, luego es removido y agregamos un "5" a la secuencia. En este momento nos detenemos porque quedan dos vértices. La secuencia del árbol es 4445.

Algoritmo para convertir una secuencia de Prüfer en un árbol

Sea {a[1], a[2], ..., a[n]} una secuencia de Prüfer:

El árbol va a tener n+2 nodos, numerados del 1 al n+2. El grado de cada nodo será igual al número de veces que éste aparezca en la secuencia más 1. Por ejemplo, en pseudo-código:

 for (i = 1; i <= n + 2; i++)
    degree[i] = 1;
 for (i = 1; i <= n; i++)
    degree[a[i]]++;

Luego, por cada número a[i] en la secuencia, encontrar j, el primer nodo con grado 1 y cuya etiqueta es la menor y agregar la arista (j, a[i]) al árbol. Decrementar los grados de a[i] y de j. En pseudo-código:

 tree = empty;
 for (i = 1; i <= n; i++) {
   for (j = 1; degree[j] != 1; j++) ;
   tree += edge (j, a[i]);
   degree[j]--;
   degree[a[i]]--;
 }

Al finalizar este bucle quedan dos nodos con grado 1 (llamémoslos u, v). Por último, agregar la arista (u,v) al árbol.^[2]

Fórmula de Cayley

Es claro que la secuencia de Prüfer de un árbol etiquetado de n vértices es una única secuencia de longitud n − 2 de los símbolos del 1 al n. Es menos obvio que dada una secuencia S de longitud n − 2 de los símbolos del 1 al n existe un único árbol etiquetado cuya secuencia de Prüfer es S. Ésto puede ser fácilmente probado por inducción.

La consecuencia inmediata es que las secuencias de Prüfer proveen una biyección entre el conjunto de árboles etiquetados de n vértices y el conjunto de secuencias de longitud n − 2 con símbolos del 1 al n. El último conjunto tiene tamaño n^{n − 2}, por lo que la existencia de esta biyección prueba la fórmula de Cayley, es decir que hay n^{n − 2} árboles etiquetados con n vértices.

Otras aplicaciones

• La fórmula de Cayley puede reforzarse para probar la siguiente afirmación:

El número de árboles de expansión en un grafo completo K_n con grados d₁,d₂,...,d_n es igual a

La prueba se sigue de la observación de que en la secuencia de Prüfer el número i aparece exactamente (d_i − 1) veces.

• La fórmula de Cayley puede generalizarse: un árbol etiquetado es un árbol de expansión de un grafo completo etiquetado. Al imponer restricciones sobre las secuencias de Prüfer enumeradas, se pueden obtener con métodos similares el número de árboles de expansión de grafos completos bipartidos. Si G es un grafo completo bipartido con vértices de 1 a n₁ en una partición y vértices n₁ + 1 a n en la otra partición, el número de árboles de expansión de G es , donde n₂ = n − n₁.

Referencias

Enlaces externos

• Prüfer code – en MathWorld