Árbol (teoría de grafos)

Árbol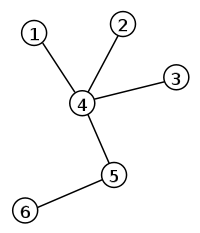
Árbol etiquetado con 6 vértices y 5 aristas. El único camino simple que conecta los vértices 2 y 6 es 2-4-5-6.
Vértices	v
Aristas	v-1
Número cromático	2 si v > 1
Propiedades	Bipartito, expandible y plano (si el conjunto de vértices es numerable)

En teoría de grafos, un árbol es un grafo en el que cualesquiera dos vértices están conectados por exactamente un camino. Un bosque es una unión disjunta de árboles. Un árbol a veces recibe el nombre de árbol libre.

Definiciones

Un árbol es un grafo simple unidireccional G que satisface alguna de las siguientes condiciones equivalentes:

• G es conexo y no tiene ciclos simples.
• G no tiene ciclos simples y, si se añade alguna arista se forma un ciclo simple.
• G es conexo y si se le quita alguna arista deja de ser conexo.
• G es conexo y el grafo completo de 3 vértices K₃ no es un menor de G.
• Dos vértices cualquiera de G están conectados por un único camino simple.

Si G tiene muchos vértices, n, entonces las definiciones anteriores son también equivalentes a cualquiera de las siguientes condiciones:

• G es conexo y tiene n − 1 aristas.
• G no tiene aristas simples y tiene n − 1 aristas.
• La cantidad de hojas de un árbol siempre es mayor o igual a la mitad de la totalidad de los nodos.

Un grafo unidireccional simple G es un bosque si no tiene ciclos simples.

Un árbol dirigido es un grafo dirigido que sería un árbol si no se consideraran las direcciones de las aristas. Algunos autores restringen la frase al caso en el que todos las aristas se dirigen a un vértice particular, o todas sus direcciones parten de un vértice particular.

Un árbol recibe el nombre de árbol con raíz si cada vértice ha sido designado raíz, en cuyo caso las aristas tienen una orientación natural hacia o desde la raíz. Los árboles con raíz, a menudo con estructuras adicionales como orden de los vecinos de cada vértice, son una estructura clave en informática; véase árbol (programación).

Un árbol etiquetado es un árbol en el que cada vértice tiene una única etiqueta. Los vértices de un árbol etiquetado de n vértices reciben normalmente las etiquetas {1,2, ..., n}.

Un árbol regular u homogéneo es un árbol en el que cada vértice tiene el mismo grado.

Propiedades

Todo árbol es a su vez un grafo bipartito. Todo árbol con sólo un conjunto numerable de vértices es además un grafo plano.

Todo grafo conexo G admite un árbol de expansión, que es un árbol que contiene cada vértice de G y cuyas aristas son aristas de G.

Dado n vértices etiquetados, hay n ⁿ⁻² maneras diferentes de conectarlos para construir un grafo. El resultado se llama fórmula de Cayley. El número de árboles con n vértices de grado d₁,d₂,...,d_n es:

que es un coeficiente multinomial.

Contar el número de árboles no etiquetados es un problema complicado. De hecho, no se conoce ninguna fórmula para el número de árboles t(n) con n vértices (debe entederse aquí el número de árboles diferentes salvo isomorfismo de grafos). Los primerlos valores de t(n) son 1, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, 551, 1301, 3159, ... (sucesión A000055 en OEIS). Otter (1948) probó que

Una fórmula más exacta para el comportamiento asintótico de t(n) implica que hay dos números α y β (α ≈ 3 y β ≈ 0.5) tales que:

Véase también

• Árbol (programación)