Grafo completo

Grafo completo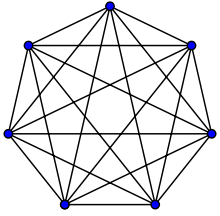
Grafo completo
Complete graph K7.svg
K7, grafo completo de 7 vértices.
Vértices n
Aristas n (n-1)/2
Diámetro 1
Cintura (girth) 3, si n ≥ 3
Automorfismos n! (Sn)
Número cromático n
Índice cromático n, si n es impar
n-1, si n es par
Propiedades (n-1)-regular
Simétrico
Vértice transitivo
Arista transitivo
Distancia unidad
Fuertemente regular
Integral

En teoría de grafos, un grafo completo es un grafo simple donde cada par de vértices está conectado por una arista.

Un grafo completo de n vértices tiene n(n − 1) / 2 aristas, y se nota Kn. Es un grafo regular con todos sus vértices de grado n − 1. Ningún grafo completo tiene lazos y está conectado totalmente, por ende, la única forma de hacer disconexo el grafo con una eliminación de vértices es aplicarla a todos.

El teorema de Kuratowski dice que un grafo planar no puede contener K5 (ó el grafo bipartito completo K3,3) y todo Kn incluye a Kn − 1, entonces ningún grafo completo Kn con n \ge 5 es planar

Ejemplos

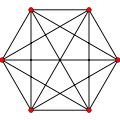
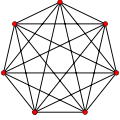
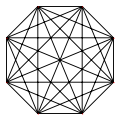
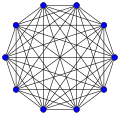
Los grafos completos de 1 a 12 vértices son los siguientes:

  • K1:0

  • K2:1

  • K3:3

  • K4:6

  • K5:10

  • K6:15

  • K7:21

  • K8:28

  • K9:36

  • K10:45

  • K11:55

  • K12:66


Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Grafo completo bipartido — Un grafo bipartido completo es aquel grafo en el que todos los vértices de la bipartición V1 están conectados a todos los vértices de la bipartición V2, y viceversa. Se denota por Kr,s al grafo bipartido completo donde V1 tiene r vértices y V2… …   Enciclopedia Universal

  • Grafo singleton — Vértices 1 Aristas 0 …   Wikipedia Español

  • Grafo bipartito completo — En teoría de grafos un grafo bipartito (o bipartido) completo es aquel Grafo bipartito en el que todos los vértices de la partición V1 están conectados a todos los vértices de la partición V2 y viceversa. Definición Un grafo bipartito completo es …   Wikipedia Español

  • Grafo plano — Grafos de ejemplo Plano No plano …   Wikipedia Español

  • Grafo — Para otros usos de este término, véase Grafo (desambiguación). Para la teoría en torno a este objeto matemático, véase Teoría de grafos. Grafo etiquetado con 6 vértices y 7 aristas. En matemáticas y ciencias de la computación, un grafo (del …   Wikipedia Español

  • Grafo ciclo — Ciclo Cn C6: Un Grafo Ciclo de longitud 6. Vertices: n Aristas: n …   Wikipedia Español

  • Grafo regular — En Teoría de grafos, un Grafo regular es un grafo donde cada vértice tiene el mismo grado o valencia. Un Grafo regular con vértices de grado k es llamado Grafo k regular o Grafo regular de grado k. Los Grafos regulares de grado hasta 2 son… …   Wikipedia Español

  • Grafo autocomplementario — El estilo de esta traducción aún no ha sido revisado por terceros. Si eres hispanohablante nativo y no has participado en esta traducción puedes colaborar revisando y adaptando el estilo de ésta u otras traducciones ya acabadas …   Wikipedia Español

  • Grafo denso — Un grafo denso, en matemáticas, es un grafo en el que el número de aristas está cercano al número de máximo de aristas. Lo opuesto, un grafo con solo algunas aristas, es un grafo disperso. La distinción entre grafos dispersos y densos es… …   Wikipedia Español

  • Grafo integral — En teoría de grafos, un grafo integral es un grafo cuyo espectro consiste enteramente de enteros. En otras palabras, un grafo es integral si todos los valores propios de su polinomio característico son enteros.[1] La noción fue introducida en… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”