- Conjunto algebraico
-
En Geometría algebraica, un conjunto algebraico es el conjunto de ceros comunes a un conjunto de polinomios.
Esto es, si S={p1, p2, ..., pt} es un conjunto de polinomios en n variables, el conjunto algebraico correspondiente a S, denotado por V(S) se define como
 .
.O de forma alterna, el conjunto de puntos tales que al ser sustituidos en cada uno de los polinomios se obtiene cero.
Cuando S consta de un sólo elemento {p}, se suele escribir V(p) en vez de V({p}).
Ejemplos
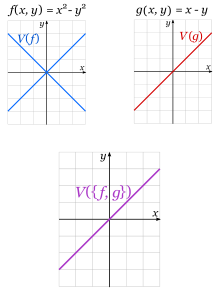
Consideremos, los polinomios
 .
.El conjunto de ceros de f, esto es, los puntos que satisfacen f(x,y)=0 es
 para cualquier valor real de a.
para cualquier valor real de a.Por otro lado, el conjunto de ceros de g es
 para cualquier valor real de a.
para cualquier valor real de a.Ambos conjuntos son por tanto ejemplos de conjuntos algebraicos (definidos por sólo un polinomio). Finalmente el conjunto algebraico definido por {f, g} es la intersección de V(f) con V(g), pues ésta contiene a los ceros comunes a ambos polinomios:
 para cualquier valor real de a.
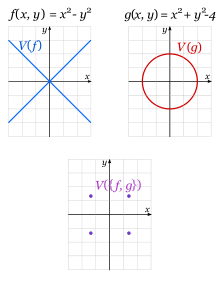
para cualquier valor real de a.Por otro lado, si
 .
.entonces V(g) es el círculo con centro en el origen y radio 2. Para estos dos polinomios,
 .
.Si bien los ejemplos considerados corresponden a polinomios en 2 variables reales, los conjuntos algebraicos se definen sobre cualquier campo F, de modo que si los polinomios tienen n variables, el conjunto algebraico correspondiente quedará formado por puntos en el espacio afín Fn.
Wikimedia foundation. 2010.