Corchete de Lagrange

Corchete de Lagrange

Corchete de Lagrange

En mecánica hamiltoniana, los corchetes de Lagrange son expresiones cercamente relacionadas con los corchetes de Poisson. Éstos fueron introducidos por Joseph Louis Lagrange en 1808–1810 como proposición de la formulación matemática de la mecánica clásica, pero comparados con los corchetes de Poisson, éstos se han dejado de usarlos.

Contenido

Definición

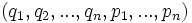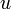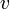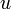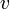Supóngase que \ (q_1, q_2, ... , q_n, p_1, ... , p_n) es un sistema de coordenadas canónicas en un espacio de fase. Si cada una esta expresada como función de dos variables \ u y \ v, entonces el corchete de Lagrange de \ u y \ v esta definido como:

[ u, v ]_{p,q} = \sum_{i=1}^n \left(\frac{\partial q_i}{\partial u} \frac{\partial p_i}{\partial v} - \frac{\partial p_i}{\partial u} \frac{\partial q_i}{\partial v} \right).

Propiedades

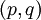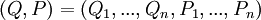  • Los corchetes de Lagrange no dependen del sistema de coordenadas canónicas \ (p, q), si \ (Q,P) = (Q_1,..., Q_n, P_1,..., P_n) es otro sistema de coordenadas canónicas, entonces tenemos que:

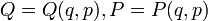
\ Q=Q(q,p), P=P(q,p)

es una transformación canónica. El corchete entonces es un invariante de la transformación, en el sentido de que:

\ [ u, v]_{q,p} = [u , v]_{Q,P}.

Por lo tanto, los subíndices suelen ser omitidos.
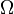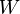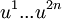  • Si \ \Omega es una forma simpléctica en un espacio de fase bidimensional \ W y \ u^1 ... u^{2n} forma un sistema de coordenadas en 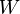\ W, entonces las coordenadas canónicas 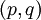\ (p,q) pueden ser expresadas como funciones de las coordenadas 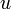\ u y la matriz de los corchetes de Lagrange:

[ u_i, u_j ]_{p,q}, \quad 1\leq i,j\leq 2n

representan los componentes de 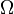\ \Omega, vistos como tensores, en las coordenadas 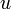\ u. Ésta matriz es la matriz inversa de la matriz formada por los corchetes de Poisson:

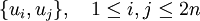
\{u_i, u_j\}, \quad 1\leq i,j\leq 2n

de las coordenadas \ u .
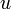  • Como un corolario de las propiedades anteriores, las coordenadas 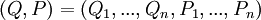\ (Q,P) = (Q_1,..., Q_n, P_1,..., P_n) en un espacio de fase son canónicas si y solo si los corchetes de Lagrange entre ellos tienen la forma:

[Q_i, Q_j]_{p,q}=0, \quad [P_i,P_j]_{p,q}=0,\quad [Q_i, P_j]_{p,q}=-[P_j, Q_i]_{p,q}=\delta_{ij}.

Véase también

Referencias

  • Cornelius Lanczos, The Variational Principles of Mechanics, Dover (1986), ISBN 0-486-65067-7.
  • Iglesias, Patrick, Les origines du calcul symplectique chez Lagrange The origins of symplectic calculus in Lagrange's work, L'Enseign. Math. (2) 44 (1998), no. 3-4, 257--277.
Obtenido de "Corchete de Lagrange"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Corchete de Poisson — Saltar a navegación, búsqueda En matemáticas y mecánica clásica, el corchete de Poisson es un importante operador de la mecánica hamiltoniana, actuando como pieza fundamental en la definición de la evolución temporal de un sistema dinámico en la… …   Wikipedia Español

  • Mecánica hamiltoniana — La mecánica hamiltoniana fue formulada en 1833 por William R. Hamilton. Como la mecánica lagrangiana, es una reformulación de la mecánica clásica. La mecánica hamiltoniana puede ser formulada por sí misma, usando los espacios simplécticos, sin… …   Wikipedia Español

  • Transformación canónica — En mecánica hamiltoniana, una transformación canónica es un cambio de coordenadas canónicamente conjugadas que preserva la forma canónica de las ecuaciones de Hamilton, aun cuando la propia forma del Hamiltoniano no queda invariante. Las… …   Wikipedia Español

  • Teorema fundamental de la geometría de Riemann — En geometría de Riemann, el teorema fundamental de la geometría de Riemann establece que dado una variedad de Riemann (o una variedad seudoriemanniana) hay una única conexión libre de torsión que preserva el tensor métrico. Tal conexión se llama… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”