- Corchete de Poisson
-
Corchete de Poisson
En matemáticas y mecánica clásica, el corchete de Poisson es un importante operador de la mecánica hamiltoniana, actuando como pieza fundamental en la definición de la evolución temporal de un sistema dinámico en la formulación hamiltoniana. Desde un punto de vista más general, el corchete de Poisson se usa para definir un álgebra de Poisson, de las que las variedades de Poisson son un caso especial. Todas éstas están nombradas en honor a Siméon-Denis Poisson.
Contenido
Definición
Sea M una variedad simpléctica, esto es, una variedad en la que existe una forma simpléctica: una forma diferencial de segundo orden ω que es a la vez cerrada (dω = 0) y no-degenerada, en el siguiente sentido: cuando se ve como un mapa
![\omega: \xi \in \mathrm{vect}[M] \rightarrow i_\xi \omega \in \Lambda^1[M]](/pictures/eswiki/55/756592c85716cb954c0ff935f867f834.png) , ω es invertible para obtener
, ω es invertible para obtener ![\tilde{\omega}: \Lambda^1[M] \rightarrow \mathrm{vect}[M]](/pictures/eswiki/101/e9ff0e93ef833677ab232b4a6ba10bdc.png) . Aquí d se usa como la derivada exterior, operador intrínseco a la estructura de la variedad M, e iξθ es la derivada interior u operación de contracción tensorial, que es equivalente a θ(ξ) en formas diferenciales de primer orden θ.
. Aquí d se usa como la derivada exterior, operador intrínseco a la estructura de la variedad M, e iξθ es la derivada interior u operación de contracción tensorial, que es equivalente a θ(ξ) en formas diferenciales de primer orden θ.Usando los axiomas del cálculo exterior, uno puede derivar:
![\ i_{[v, w]} \omega = d(i_v i_w \omega) + i_v d(i_w \omega) - i_w d(i_v \omega) - i_w i_v d\omega](/pictures/eswiki/51/3f255d01672ff7c94e97088e5d16f94e.png)
Aquí [v,w] denota el corchete de Lie en campos vectoriales suaves, que esencialmente define la estructura de la variedad de M.
Si v es tal que d(ivω) = 0, se le puede llamar ω-cocerrado (o simplemente cocerrado). A su vez, si se cumple ivω = df para alguna función f, podemos llamar a v ω-coexacta (o simplemente coexacta). Dado que dω = 0, esto implica que el corchete de Lie de dos vectores cocerrados siempre es un campo vectorial coexacto, ya que cuando v y w son ambos cocerrados, el único término no nulo en la expresión es d(iviwω). Y como la derivada exterior obedece
 , todos los campos vectoriales coexactos son cocerrados, y por eso el corchete de Lie es cerrado tanto en el espacio de los campos vectoriales cocerrados como en el subespacio de éste consistente en los campos vectoriales coexactos. En el lenguaje del álgebra abstracto, los campos vectoriales cocerrados forman un subálgebra del álgebra de Lie de los campos vectoriales suaves en M, y los campos vectoriales coexactos forman un álgebra ideal de este subálgebra.
, todos los campos vectoriales coexactos son cocerrados, y por eso el corchete de Lie es cerrado tanto en el espacio de los campos vectoriales cocerrados como en el subespacio de éste consistente en los campos vectoriales coexactos. En el lenguaje del álgebra abstracto, los campos vectoriales cocerrados forman un subálgebra del álgebra de Lie de los campos vectoriales suaves en M, y los campos vectoriales coexactos forman un álgebra ideal de este subálgebra.Dada la existencia del mapa inverso
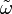 , todas las funciones reales suaves f en M pueden ser asociadas a un campo vectorial coexacto
, todas las funciones reales suaves f en M pueden ser asociadas a un campo vectorial coexacto 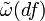 . (Dos funciones están asociadas con el mismo campo vectorial si, y sólo si, su diferencia está en el núcleo de d, esto es, constante en cada componente conectada de M.) Así, definimos el corchete de Poisson en (M,ω) como una operación bilinear en las funciones diferenciables sobre las que las funciones (suaves) de
. (Dos funciones están asociadas con el mismo campo vectorial si, y sólo si, su diferencia está en el núcleo de d, esto es, constante en cada componente conectada de M.) Así, definimos el corchete de Poisson en (M,ω) como una operación bilinear en las funciones diferenciables sobre las que las funciones (suaves) de 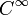 forman un álgebra. Esto está dado por:
forman un álgebra. Esto está dado por: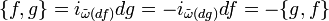
Esta simetría sesgada del corchete de Poisson está asegurada por los axiomas del cálculo exterior y la condición dω = 0. Como el mapa
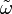 es linear en todo punto y de simetría sesgada, algunos autores lo asocian a un bivector, que no es un objeto frecuentemente encontrado en el cálculo exterior. En esta forma se llama el bivector de Poisson o la estructura de Poisson en la variedad simpléctica, y se denota como
es linear en todo punto y de simetría sesgada, algunos autores lo asocian a un bivector, que no es un objeto frecuentemente encontrado en el cálculo exterior. En esta forma se llama el bivector de Poisson o la estructura de Poisson en la variedad simpléctica, y se denota como 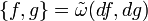 .
.El corchete de Poisson en funciones suaves se corresponde con el corchete de Lie en campos vectoriales coexactos y hereda toda sus propiedades. Por lo que satisface la Identidad de Jacobi:
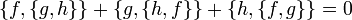
El corchete de Poisson {f,_} respecto a un campo escalar f se corresponde con la derivada de Lie respecto a
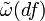 . Por lo que es una derivada, y así, satisface la Regla de Leibniz:
. Por lo que es una derivada, y así, satisface la Regla de Leibniz:
Una propiedad fundamental de las variedades es que el conmutador de las operaciones de derivada de Lie sobre dos campos vectoriales es equivalente a la derivada de Lie respecto de algún campo vectorial, que se será su corchete de Lie. El rol paralelo del corchete de Poisson es aparente haciendo una ordenación de la identidad de Jacobi:
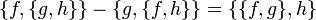
Si el corchete de Poisson de f y g se anula ({f,g} = 0), entonces se dice que f y g están en involución mutua, y las operaciones de hacer el corchete de Poisson respecto de f y g conmutan.
Coordenadas canónicas
El corchete de Poisson se puede expresar en coordenadas canónicas
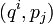 del espacio de fases
del espacio de fases  :
:(*)
![\{\tilde{f},\tilde{g}\} = \sum_{i=1}^{N} \left[
\frac{\part \tilde{f}}{\part q^{i}} \frac{\part \tilde{g}}{\part p_{i}} -
\frac{\part \tilde{f}}{\part p_{i}} \frac{\part \tilde{g}}{\part q^{i}}
\right]](/pictures/eswiki/53/5c66e175af49fc0e73b5c12f3f99effe.png)
Más formalmente si
 es una carta local, asociada a las coordenadas canónicas definidas anteriormente, es decir:
es una carta local, asociada a las coordenadas canónicas definidas anteriormente, es decir: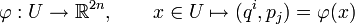
El corchete de Poisson el pullback de la anterior aplicación dada en ():
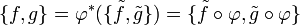
Ecuaciones del movimiento
Las ecuaciones de movimiento de Hamilton-Jacobi tienen una expresión equivalente en términos del corchete de Poisson. Esto se puede demostrar directamente tomando unas coordenadas explícitas. Imaginemos que f(q,p,t) es una función en la variedad. Entonces se tiene que
Entonces, llamando a p = p(t) y q = q(t) las soluciones de las ecuaciones de Hamilton-Jacobi
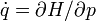 y
y  , uno puede escribir
, uno puede escribirAsí, la evolución temporal de una función f en una variedad simpléctica puede darse como una familia uniparamétrica de variemorfismos, con el tiempo t siendo el parámetro. Desechando las coordenadas, se tiene
El operador
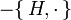 se conoce como el liouvilliano.
se conoce como el liouvilliano.Constantes de movimiento
Un sistema dinámico integrable tiene que tener constantes de movimientos además de la energía. Tales constantes conmutarán con el hamiltoniano bajo el corchete de Poisson. Imaginemos que la función f(q,p) es una constante de movimiento. Esto implica que si q(t),p(t) es una trayectoria o solución de las ecuaciones de movimiento de Hamilton-Jacobi, entonces se tiene que
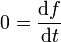 a lo largo de dicha trayectoria. Por lo que
a lo largo de dicha trayectoria. Por lo quedonde, como arriba, los pasos intermedios se realizan aplicando las ecuaciones de movimiento. Esta ecuación se conoce como la ecuación de Liouville. El contenido del teorema de Liouville es que la evolución temporal de una medida (o función de distribución en el espacio de fases) está dado por lo anterior.
Para que un sistema hamiltoniano sea completamente integrable, todas sus constantes de movimiento deben estar en involución mutua.
Álgebra de Lie
Los corchetes de Poisson son anticonmutativos. También satisfacen la identidad de Jacobi. Esto hace que el espacio de las funciones suaves de una variedad simpléctica sea un álgebra de Lie de dimensión infinita con el corchete de Poisson actuando como el corchete de Lie. El correspondiente grupo de Lie es el grupo de simplectomorfismos de las variedades simplécticas (también conocido como transformaciones canónicas).
Dado un campo vectorial diferenciable X en el entorno tangente, sea PX su momento conjugado. El mapa de los momentos conjugados es un álgebra de Lie antihomomorfa desde el corchete de Poisson al corchete de Lie:
Esto es un resultado importante que merece la pena demostrar. Escribamos un campo escalar X en el punto q del espacio de configuración como
donde
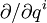 se refiere al marco de coordenadas locales. El momento conjugado de X tiene la forma
se refiere al marco de coordenadas locales. El momento conjugado de X tiene la formadonde pi son las funciones momento conjugadas de las coordenadas. Entonces se tiene, para un punto (q,p) en el espacio de fases,
Lo anterior se mantiene para todos los (q,p), llegando al resultado deseado.
Véase también
Categoría: Mecánica hamiltoniana
Wikimedia foundation. 2010.

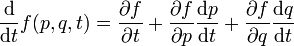

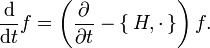
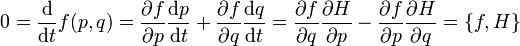
![\{P_X,P_Y\}=-P_{[X,Y]}.\,](/pictures/eswiki/53/53a18960c0b08fc9a6d356efe3bd71c5.png)
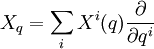
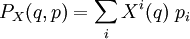
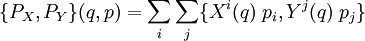
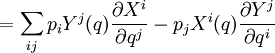
![= - \sum_i p_i \; [X,Y]^i(q)](/pictures/eswiki/48/0791d653f917960fe59c04b1bbd549ad.png)
![= - P_{[X,Y]}(q,p). \,](/pictures/eswiki/102/f19e0ab6d80bbea66155331a4c9f6967.png)