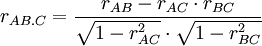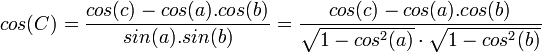Correlación parcial

Correlación parcial

Correlación parcial

El coeficiente de correlación parcial, anotado aquí rAB.C, permite conocer el valor de la correlación entre dos variables A y B, si la variable C había permanecido constante para la serie de observaciones consideradas.

Dicho de otro modo, el coeficiente de correlación parcial rAB.C es el coeficiente de correlación total entre las variables A y B cuando se les retiró su mejor explicación lineal en término de C.

Contenido

Fórmula

r_{AB.C} = \dfrac{ r_{AB} - r_{AC}\cdot r_{BC}}{\sqrt{ 1-r_{AC}^2}\cdot\sqrt{ 1-r_{BC}^2}}

Demostración geométrica

La demostración más rápida de la fórmula consiste en apoyarse en la interpretación geométrica de la correlación (coseno).

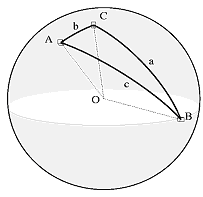
Las series de observaciones A, B y C, una vez centradas reducidas, son vectores centrados OA, el OB, OC de longitud unidad:


PartialCorrelation.png

Sus extremidades determinan un triángulo esférico ABC, el que los lados a, b y c " son los arcos de grandes círculo BC, AC y AB. Los coeficientes de correlaciones entre estos vectores son rBC = cos(a), rAC = cos(b) y rAB = cos(c). Entonces la ley fundamental de los triángulos esféricos da, para el ángulo C, la relación siguiente entra coseno:

cos(C) = \dfrac{cos(c)-cos(a).cos(b)}{sin(a).sin(b)} = \dfrac{cos(c)-cos(a).cos(b)} {\sqrt{1-cos^2(a)}\cdot\sqrt{1-cos^2(b)}}

Lo mismo que c está el ángulo entre los puntos A y B, vistos por el centro de la esfera, C está el ángulo esférico entre los puntos A y B, vistos por el punto " C " en la superficie de la esfera, y rAB.C = cos(C) es la « correlación parcial » entre A y B cuando C es fijado.

Véase también

Referencias

R. A. Fisher (1924). "The distribution of the partial correlation coefficient". Metron 3 (3–4): 329–332.

Obtenido de "Correlaci%C3%B3n parcial"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Iconografía de las correlaciones — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… …   Wikipedia Español

  • Trastorno límite de la personalidad — «Borderline» redirige aquí. Para otras acepciones, véase Borderline (desambiguación). Trastorno límite de la personalidad Clasificación y recursos externos …   Wikipedia Español

  • Elecciones en Madrid durante la Segunda República Española — Durante la Segunda República hubo cuatro procesos electorales de carácter nacional: tres a Cortes y uno para elección de compromisarios para elegir al Presidente de la …   Wikipedia Español

  • Propagación de errores — Saltar a navegación, búsqueda En Estadística, la propagacion de errores (o propagación de incertidumbre) es el efecto de variables de incertidumbre (o errores) en la incertidumbre de una función matemática basada en ellos. Cuando las variables… …   Wikipedia Español

  • Polarización electromagnética — Para la polarización en electrostática, véase polarización eléctrica. La polarización electromagnética es un fenómeno que puede producirse en las ondas electromagnéticas, como la luz, por el cual el campo eléctrico oscila sólo en un plano… …   Wikipedia Español

  • Cuenta larga — Saltar a navegación, búsqueda Detalle que muestra tres columnas de glifos del segundo siglo antes de la era cristiana. La columna de la izquierda representa la fecha en Cuenta Larga 8.5.16.9.9 (leyendo de arriba hacia abajo), correspondiente al… …   Wikipedia Español

  • Acceso múltiple por división de código — «CDMA» redirige aquí. Para el organismo andaluz, véase Centro de Documentación Musical de Andalucía. La multiplexación por división de código, acceso múltiple por división de código o CDMA (del inglés Code Division Multiple Access) es un término… …   Wikipedia Español

  • Rongo rongo — Saltar a navegación, búsqueda Símbolos Rongo rongo Se conoce con el nombre de rongo rongo a un supuesto sistema de escritura tallado con ‘puntas de obsidiana o dientes de tiburón’, en su mayoría sobre las tablillas de madera. Los habitantes de la …   Wikipedia Español

  • Varios intentos de descifrar el significado de los kohau rongo rongo — El kohau rongorongo, en el curso de unos 135 140 años, ha sido objeto de investigación intensa, así como objeto de un debate encendido por parte de mucha gente, tanto de entrenamiento sólido académico (lingüístico, epigráfico, etnológico y… …   Wikipedia Español

  • Aborto inducido — Para otros usos de este término, véase aborto. Aborto inducido Bajo relieve en Angkor Wat, Camboya, c. 1150, que representa a un demonio golpeando el abdomen de una m …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”