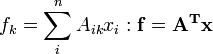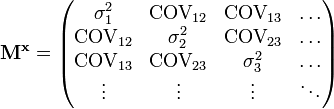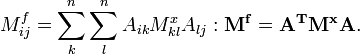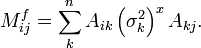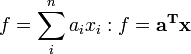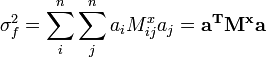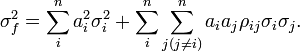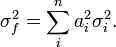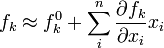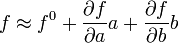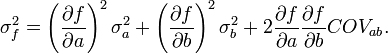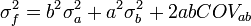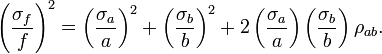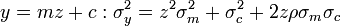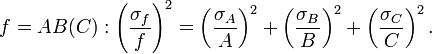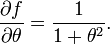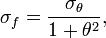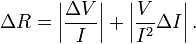- Propagación de errores
-
Propagación de errores
En Estadística, la propagacion de errores (o propagación de incertidumbre) es el efecto de variables de incertidumbre (o errores) en la incertidumbre de una función matemática basada en ellos. Cuando las variables son los valores de mediciones experimentales tienen incertidumbre debido a la medición de limitaciones (por ejemplo, instrumento de precisión), que se propagan a la combinación de variables en la función.
La incertidumbre es normalmente definida por el error absoluto. La incertidumbre también puede ser definida por el error relativo Δx/x, que usualmente es escrito como un porcentaje.
Más comúnmente, el error en una cantidad, Δx, está dado por la desviación estándar, σ. La desviación estándar es la raíz cuadrada positiva de la varianza, σ2. El valor de una cantidad y su error son, a menudo, expresados como
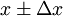 . Si la distribución de probabilidad estadística de la variable es conocida o puede ser asumida, es posible derivar el intervalo de confianza para describir la región dentro de la cual el valor verdadero de la variable puede ser encontrado. Por ejemplo, el intervalo de confianza de 68% de una variable perteneciente a una distribución normal es ± una desviación estándar del valor, esto es, existe un 68% de probabilidad que el valor verdadero se encuentre en la región
. Si la distribución de probabilidad estadística de la variable es conocida o puede ser asumida, es posible derivar el intervalo de confianza para describir la región dentro de la cual el valor verdadero de la variable puede ser encontrado. Por ejemplo, el intervalo de confianza de 68% de una variable perteneciente a una distribución normal es ± una desviación estándar del valor, esto es, existe un 68% de probabilidad que el valor verdadero se encuentre en la región 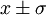 . Si las variables están correlacionadas, entonces la covarianza debe ser tomada en cuenta.
. Si las variables están correlacionadas, entonces la covarianza debe ser tomada en cuenta.Contenido
Combinaciones lineales
Sea
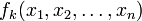 un conjunto de m funciones que son combinaciones lineales de n variables
un conjunto de m funciones que son combinaciones lineales de n variables 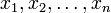 con coeficientes de combinación
con coeficientes de combinación 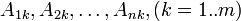 .
.y sea la matriz de covarianza en x denotada por
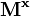 .
.Entonces, la matriz de covarianaza
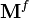 , de f está dada por
, de f está dada porEsta es la expresión más general para la propagación del error de un conjunto de variables a otro. Cuando los errores en x no están correlacionados, la expresión general se simplifica a
Obsérvese que, incluso aunque los errores en x puedan estar no correlacionados, sus errores en f siempre lo están. Las expresiones generales para una función simple, f, son un poco más sencillas.
Cada término de covarianza, Mij puede ser expresado en términos del coeficiente de correlación
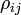 por
por 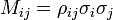 , con lo que una expresión alternativa para la varianza de f es
, con lo que una expresión alternativa para la varianza de f esEn el caso que las variables x estén no correlacionadas, esto se simplifica más aún a
Combinaciones no lineales
Cuando f es un conjunto de una combinación no lineal de las variables x, generalmente debe ser linealizada por aproximación a una expansión de la serie de Taylor de primer orden, aunque en algunos casos pueden derivarse fórmulas exactas que no dependen de la expansión.[1]
Donde
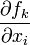 denota la derivada parcial de fk con respecto a la variable i-ésima. Puesto que f0k es una constante, no contribuye al error en f. En consecuencia, la propagación del error sigue el caso lineal, visto anteriormente, pero reemplazando los coeficientes lineales, Aik y Ajk por las derivadas parciales,
denota la derivada parcial de fk con respecto a la variable i-ésima. Puesto que f0k es una constante, no contribuye al error en f. En consecuencia, la propagación del error sigue el caso lineal, visto anteriormente, pero reemplazando los coeficientes lineales, Aik y Ajk por las derivadas parciales, 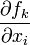 y
y 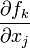 .
.Ejemplo
Cualquier función no lineal, f(a,b), de dos variables, a y b, puede ser expandida como
de donde se tiene
En el caso particular que
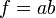 ,
, 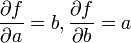 . Entonces
. Entonceso
Advertencias
La estimación de errores para funciones no lineares está sesgada debido al uso de series de expansión truncas. La extensión de este sego depende de la naturaleza de la función; por ejemplo, el sesgo en el error calculado para log x se incrementa si x aumenta, dado que la expansión de 1+x es una buena aproximación solo si x es pequeña.
En aplicaciones de data correspondiente, es a menudo posible asumir que los errores de medida no están correlacionados; sin embargo, los parámetros derivados de estas mediciones, tales como parámetros Mínimos cuadrados, estarán correlacionados. Por ejemplo, en una regresión lineal, los errores en la pendiente y la intercepción estarán correlacionados y esta correlación debe ser tomada en cuenta cuando se derive el error en un valor calculado.
En el caso especial de la inversa 1 / B donde B = N(0,1), la distribución es una distribución de Cauchy y no hay una varianza definible. Para tales distribuciones de ratio, puede haber probabilidades definidas para intervalos que pueden ser definidos o bien por simulación Monte Carlo o, en algunos casos, usando la transformación Geary-Hinkley.[2]
Fórmulas de ejemplo
Esta tabla muesta las varianzas de funciones simples de las variables reales
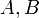 con desviaciones estándar
con desviaciones estándar 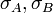 , coeficiente de correlación
, coeficiente de correlación 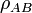 y constantes de valores reales, conocidas precisamente,
y constantes de valores reales, conocidas precisamente, 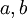 .
.-
Función 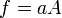
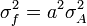
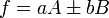
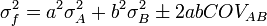
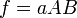
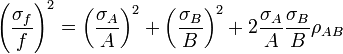
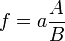
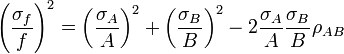
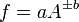
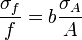
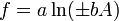
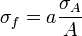
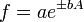
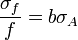
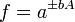
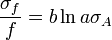
Para variables no correlacionadas, los términos de covarianza son cero. Puede derivarse expresiones para funciones más complicadas por combinación de funciones más simples. Por ejemplo, la multiplicación repetida, asumiendo ninguna correlación, conduce a:
Derivadas parciales
Dados
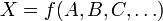
-
Error Absoluto Varianza 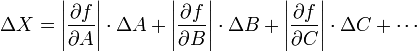
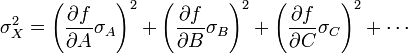 [3]
[3]
Ejemplos
Función tangente inversa
Se puede calcular la propagación de la incertidumbre para la función tangente inversa como ejemplo del uso de derivadas parciales para la propagación del error.
Definiendo
- f(θ) = arctanθ,
donde σθ es la incertidumbre absoluta en la medida de θ.
La derivada parcial de f(θ) con respecto a θ es
En consecuencia, la incertidumbre propagada es
donde σf es la incertidumbre absoluta propagada.
Medición de la resistencia
Una aplicación práctica es un experimento en el que se mide la corriente, I, y el voltaje de un resistor con el fin de determinar la resistencia, R, usando la ley de Ohm, R = V / I.
Dadas las variables medidas con sus incertidumbres, I±ΔI y V±ΔV, la incertidumbre en la cantidad calculada, ΔR, es
Referencias
- ↑ Leo Goodman (1960). «On the Exact Variance of Products» Journal of the American Statistical Association. Vol. 55. n.º 292. pp. 708–713. DOI 10.2307/2281592.
- ↑ Jack Hayya, Donald Armstrong y Nicolas Gressis (July de 1975). «A Note on the Ratio of Two Normally Distributed Variables» Management Science. Vol. 21. n.º 11. pp. 1338–1341.
- ↑ [Lindberg] (2009-10-05). «Uncertainties and Error Propagation» (en eng). Uncertainties, Graphing, and the Vernier Caliper págs. 1. Rochester Institute of Technology. Archivado desde el original, el 2004-11-12. Consultado el 2007-04-20. «The guiding principle in all cases is to consider the most pessimistic situation.»
Enlaces externos
- Incertidumbre y propagación de errores, Apéndice V del Manual de Laboratorio de Mecánica, Case Western Reserve University.
- Una discusión detallada de las medidas y la propagación de la incertidumbre explica los beneficios de usar fórmulas de propagación de errores y simulaciones Montecarlo, en lugar de simple aritmética significativa.
Véase también
Categorías: Análisis numérico | Teoría estadística
Wikimedia foundation. 2010.