Trigonometría esférica

Trigonometría esférica
Triángulo esférico trirectángulo (sus ángulos suman : 270°).

La trigonometría esférica es la parte de la geometría esférica que estudia los polígonos que se forman sobre la superficie de la esfera, en especial, los triángulos. La resolución de triángulos esféricos tiene especial relevancia en astronomía náutica y navegación para determinar la posición de un buque en altamar mediante la observación de los astros.

Contenido

La esfera

Una esfera E, de centro en el punto (a,b,c) y radio k, es el dominio de ℝ³ definido por todos aquellos puntos en el espacio tridimensional que cumplen con la siguiente definición:

E = \{\ (x,y,z) \in \mathbb{R}^3 \ | \ (x - a)^2 + (y - b)^2 + (z - c)^2 = k^2\}

Círculo máximo

Distancia ortodrómica entre dos puntos a lo largo de un círculo máximo sobre la superficie de una esfera.
Artículo principal: Círculo máximo

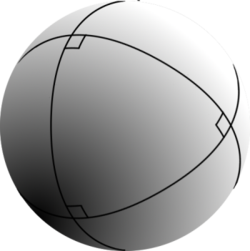
La intersección de una esfera con un plano que contenga su centro genera un círculo máximo y una circunferencia máxima sobre la superficie de la esfera. Un círculo máximo divide a la esfera en dos hemisferios iguales. La distancia entre dos puntos de la superficie de la esfera, unidos por un arco de círculo máximo, es la menor entre ellos y se denomina distancia ortodrómica.

Como ejemplos de círculos máximos en la superficie de la Tierra tenemos los meridianos o la línea del ecuador.

Volumen y superficie de la esfera

El volumen de una esfera es el volumen de revolución engendrado por un semicírculo que gira alrededor del diámetro. Según esta definición, si su radio es r, su volumen será:

\!V = \frac{4}{3}\pi r^3

La superficie es la superficie lateral de un cuerpo de revolución y vendrá dada por:

\!A = 4\pi r^2

Dominio sobre la superficie esférica

Un dominio de superficie esférica es un recinto o área sobre la superficie de la esfera limitado por curvas contenidas en dicha superficie.

Triángulo esférico

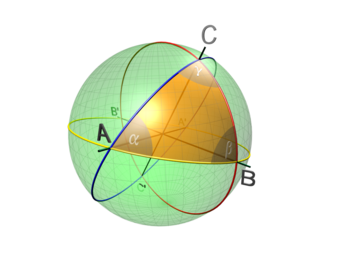
Triángulo esférico.

Si tres puntos de la superficie esférica son unidos por arcos de círculo máximo menores a 180º, la figura obtenida se denomina triángulo esférico. Los lados del polígono así formado se expresan por conveniencia como ángulos cuyo vértice es el centro de la esfera y no por su longitud. Este arco medido en radianes y multiplicado por el radio de la esfera es la longitud del arco. En un triángulo esférico los ángulos cumplen que: 180° < \alpha\! + \beta\! + \gamma\! < 540°

Fórmulas fundamentales

\alpha\!: ángulo formado entre los arcos AC y AB

\beta\!: ángulo formado entre los arcos AB y BC

\gamma\!: ángulo formado entre los arcos AC y BC

Fórmula del coseno

\cos CB= \cos AC\; \cos AB + {\rm{sen}} AC\; {\rm{sen}}AB\; \cos \alpha \!

Fórmula del seno

\frac{{\rm{sen}} CB}{{\rm{sen}}\alpha}=\frac{{\rm{sen}} AC}{{\rm{sen}}\beta}=\frac{{\rm{sen}} AB}{{\rm{sen}}\gamma}

Los senos de los lados son proporcionales a los senos de los ángulos opuestos.

Fórmula de la cotangente

La fórmula de la cotangente también se denomina fórmula de los elementos consecutivos. Ver en la figura los siguientes elementos consecutivos:

ángulo \alpha\!; lado AB; ángulo \beta\!; lado BC.

\cos \beta \cos AB ={\rm{sen}} \beta \cot \alpha\! - {\rm{sen}} AB \cot CB

Cosenos de los elementos medios, es igual a: seno del ángulo medio por la cotangente del otro ángulo, menos seno del lado medio por la cotangente del otro lado.

Fórmula de Bessel

Desde las fórmulas de los cosenos, obtenidas en la sección anterior, se pueden obtener de inmediato un conjunto de varias fórmulas conocidas como "relaciones del seno por el coseno" o también denominadas Fórmulas de Bessel, o tercera fómula de Bessel. Fueron deducidas por primera vez por el gran matemático Friedrich Wilhelm Bessel (Westfalia, Alemania, 1784-Kaliningrado, Rusia, 1846).

cos( a / k ) = cos( b / k )· cos( c / k ) + sen( b / k )· sen( c / k) · cos( A )

cos( b / k ) = cos( c / k )· cos( a / k ) + sen( c / k )· sen( a / k )· cos( B )

cos( c / k ) = cos( a / k )· cos( b / k ) + sen( a / k )· sen( b / k )· cos( C )

El conjunto de las fórmulas de Bessel puede escribirse, para la esfera de radio unidad, esto es, la esfera trigonométrica, de la forma:

sen c · cos B = cos b · sen a - cos a · sen b · cos C

sen c · cos A = cos a · sen b - cos b · sen a · cos C

sen b · cos A = cos a · sen c - cos c · sen a · cos B

sen b · cos C = cos c · sen a - cos a · sen c · cos B

sen a · cos B = cos b · sen c - cos c · sen b · cos A

sen a · cos C = cos c · sen b - cos b · sen c · cos A

Presentación matricial de las fórmulas del triángulo esférico

El conjunto de las fórmulas del seno, del coseno (llamadas por algunos segunda y primera fórmula de Bessel), y la (tercera) fórmula de Bessel, pueden expresarse de forma matricial:

\begin{vmatrix} cos(a) \\ sen(a) sen(B) \\ sen(a) cos(B) \end{vmatrix} = \begin{vmatrix} cos(c) & 0 & sen(c) \\ 0 & 1 & 0 \\ sen(c) & 0 & -cos(c) \end{vmatrix} . \begin{vmatrix} cos(b) \\ sen(b) sen(A) \\ sen(b) cos(A) \end{vmatrix}

siendo a, b y c los lados; y A, B y C los ángulos del triángulo esférico.

Triángulo esférico rectángulo

Al triángulo esférico con al menos un ángulo recto, se lo denomina triángulo rectángulo. En un triángulo esférico sus tres ángulos pueden ser rectos, en cuyo caso su suma es 270°. En todos los otros casos esa suma excede los 180° y a ese exceso se lo denomina exceso esférico; se expresa por la fórmula: E: E = \alpha\!+\beta\!+\gamma\! − 180°.

Cualquier triángulo esférico puede descomponerse en dos triángulos esféricos rectángulos.

Pentágono de Neper

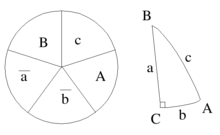
Pentágono de Neper.

El pentágono de Neper es una regla nemotécnica para resolver triángulos esféricos rectángulos; toma este nombre en memoria del científico inglés John Napier, y se construye de la siguiente forma:

Se colocan en cada sector circular: cateto - ángulo - cateto - ángulo - cateto, consecutivamente, tal como aparecen ordenados en el triángulo, exceptuando el ángulo recto C.

Se remplazan los ángulos B, C, y la hipotenusa a por sus complementarios:

B por (90° - B)
C por (90° - C)
a por (90° - a)

Se establecen dos reglas:

  • el seno de un elemento es igual al producto de las tangentes de los elementos adyacentes:
seno(a) = tg(b) tg(90° - B), o su equivalente: seno(a) = tg(b) ctg(B)
  • el seno de un elemento es igual al producto de los cosenos de los elementos opuestos:
seno(a) = coseno(90° - A) coseno(90° - c), o su equivalente: seno(a) = seno(A) seno(c)

Véase también

Bibliografía

  • Apuntes de trigonometría esférica. Escuela Nacional de Náutica Manuel Belgrano (Argentina).
  • Apuntes de Trigonometría esférica. Universidad de Cádiz.
  • Astronomía Náutica (tomo primero). Luis Virgile. Imprenta Escuela Naval Militar (Argentina).

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • trigonometría esférica — ► locución MATEMÁTICAS La que trata de los triángulos esféricos …   Enciclopedia Universal

  • Trigonometría — La trigonometría es una rama de la matemática, cuyo significado etimológico es la medición de los triángulos . Deriva de los términos griegos τριγωνο trigōno triángulo y μετρον metron medida.[1] En términos generales, la trigonometría es el… …   Wikipedia Español

  • trigonometria — s. f. 1. Ciência que ensina a medir os triângulos. v Trigonometria esférica (triângulos esféricos). 2. Trigonometria retilínea (triângulos planos) …   Dicionário da Língua Portuguesa

  • trigonometría — (Del gr. τριγωνομετρία). f. Parte de las matemáticas que trata del cálculo de los elementos de los triángulos planos y esféricos. trigonometría esférica. f. La que trata de los triángulos esféricos. trigonometría plana. f. La que trata de los… …   Diccionario de la lengua española

  • Trigonometría — (Del gr. trigonos, trígono + metron, medida.) ► sustantivo femenino 1 MATEMÁTICAS Parte de las matemáticas dedicada al estudio de las relaciones entre las amplitudes de los ángulos y las longitudes de los segmentos que sus lados determinan en las …   Enciclopedia Universal

  • Geometría esférica — En una esfera, la suma de los ángulos de un triángulo no es igual a 180°. Una esfera no es un espacio euclidiano, pero localmente las leyes de la geometría euclidiana son buenas aproximaciones. En un pequeño triángulo en la cara de la Tierra, la… …   Wikipedia Español

  • Teorema del coseno — El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que se utiliza, normalmente, en trigonometría. El teorema relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado …   Wikipedia Español

  • Fórmula del Haversine — Este artículo fue creado a partir de la traducción del artículo Haversine formula de la Wikipedia en inglés, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL. Seno, coseno y verseno de θ en base a la circunferencia… …   Wikipedia Español

  • Hiparco de Nicea — Hiparco de Nicea. Hiparco fue un astrónomo, geógrafo y matemático griego (nacido en Nicea alrededor de 190 a. C. y muere alrededor de 120 a. C.). Nace dos años antes de la muerte de Eratóstenes, del que fue sucesor en la… …   Wikipedia Español

  • Nasir al-Din al-Tusi — Nasir al Din Tusi en un sello iraní conmemorando el 700 aniversario de su muerte. Abu Jafar Muhammad Ibn Muhammad Ibn al Hasan Nasir al Din al Tusi, conocido como Nasir al Din al Tusi (1201–1274 cerca de Bagdad) fue un científico persa chií.… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”