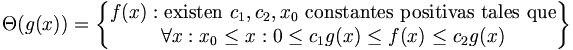- Cota ajustada asintótica
-
Cota ajustada asintótica
En análisis de algoritmos una cota ajustada asintótica es una función que sirve de cota tanto superior como inferior de otra función cuando el argumento tiende a infinito. Usualmente se utiliza la notación Θ(g(x)) para referirse a las funciones acotadas por la función g(x).
Más formalmente se define:
Una función f(x) pertenece a Θ(g(x)) cuando existen constantes positivas c1 y c2 tales que a partir de un valor x0 f(x) se encuentra atrapada entre c1g(x) y c2g(x). Quiere decir que las funciones f y g son iguales a partir de un valor dado salvo por una factor constante. Por tanto tiene sentido tomar a g como un representante de f.
A pesar de que Θ(g(x)) está definido como un conjunto, se acostumbra escribir f(x)=Θ(g(x)) en lugar de f(x)∈Θ(g(x)). Muchas veces también se habla de la función x² en lugar de h(x)=x² siempre que esté claro cual es el parámetro de la función dentro de la expresión. En la gráfica se da un ejemplo esquemático de cómo se comportan c1g(x) y c2g(x) con respecto a f(x) cuando x tiende a infinito.
La cota ajustada asintótica tiene relación con las cotas superior e inferior asintóticas (respectivamente las notaciones O y Ω):
- f(x) = Θ(g(x)) si y solo si f(x) = O(g(x)) y f(x) = Ω(g(x))
Ejemplos
- La función f(x) = x+10 puede ser acotada por la función g(x) = x. Para demostrarlo basta notar que para todo valor de x≥1 se cumple que g(x)≤f(x)≤11g(x), es decir x ≤ x+10 ≤ 11x . Por lo tanto x+10 = Θ(x).
Véase también
Bibliografía
- Introduction to Algorithms, Second Edition by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein
Categorías: Análisis asintótico | Complejidad computacional
Wikimedia foundation. 2010.