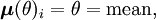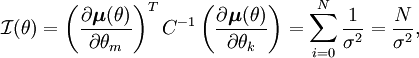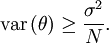- Cota de Cramér-Rao
-
Cota de Cramér-Rao
En estadística, la cota de Cramér-Rao (abreviada CRB por sus siglas del inglés) o cota inferior de Cramér-Rao (CRLB), llamada así en honor a Harald Cramér y Calyampudi Radhakrishna Rao, expresa una cota inferior para la varianza de un estimador insesgado, basado en la información de Fisher.
Establece que la inversa multiplicativa de la información de Fisher de un parámetro θ,
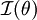 , es una cota inferior para la varianza de un estimador insesgado del parámetro (denotado mediante
, es una cota inferior para la varianza de un estimador insesgado del parámetro (denotado mediante 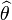 ).
).En algunos casos, no existe un estimador insesgado que alcance la cota inferior.
A esta cota se la conoce también como la desigualdad de Cramér-Rao o como la desigualdad de información.
Contenido
Condiciones de regularidad
La cota depende de dos condiciones de regularidad débiles de la función de densidad de probabilidad, f(x;θ), y del estimador T(X):
- La información de Fisher siempre está definida; en otras palabras, para todo x tal que f(x;θ) > 0,
- es finito.
- Las operaciones de integración con respecto a x y de diferenciación con respecto a θ pueden intercambiarse en la esperanza de T; es decir,
- siempre que el miembro derecho de la ecuación sea finito.
En algunos casos, un estimador sesgado puede tener tanto varianza como error cuadrático medio por debajo de la cota inferior de Cramér-Rao (la cota inferior se aplica solo a estimadores insesgados).
Si se extiende la segunda condición de regularidad a la segunda derivada, entonces se puede usar una forma alternativa de la información de Fisher para obtener una nueva desigualdad de Cramér-Rao
En algunos casos puede resultar más sencillo tomar la esperanza con respecto a la segunda derivada que tomarla respecto del cuadrado de la primera derivada.
Parámetros múltiples
Extendiendo la cota de Cramér-Rao para múltiples parámetros, defínase el vector columna de parámetros
con función de densidad de probabilidad
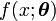 que satisface las dos condiciones de regularidad definidad anteriormente.
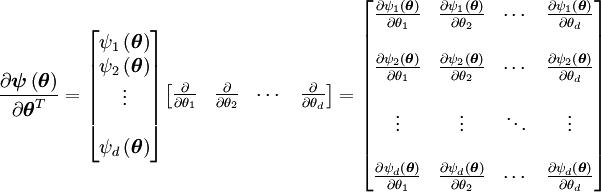
que satisface las dos condiciones de regularidad definidad anteriormente.La matriz de información de Fisher es una matriz de dimensión
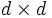 con elementos
con elementos 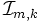 definidos según
definidos segúnentonces, la cota de Cramér-Rao bound es
donde
Y
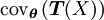 es una matriz semi-definida positiva, es decir
es una matriz semi-definida positiva, es decirSi
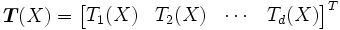 es un estimador insesgado (es decir,
es un estimador insesgado (es decir, 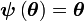 ) entonces la cota de Cramér-Rao es
) entonces la cota de Cramér-Rao esEjemplos
Distribución normal multivariada
Para el caso de una distribución normal multivariada de dimensión d
con función de densidad de probabilidad
La matriz de información de Fisher tiene elementos
donde "tr" se refiere a la traza de una matriz.
Sea w[n] ruido blanco gaussiano (una muestra de N observaciones independientes) con varianza σ2
Donde
y
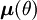 tiene N (el número de observaciones independientes) términos.
tiene N (el número de observaciones independientes) términos.Entonces la matriz de información de Fisher es de dimensión 1 × 1
y por lo tanto la cota de Cramér-Rao es
Categorías: Desigualdades | Estimación estadística
Wikimedia foundation. 2010.

![\mathrm{var} \left(\widehat{\theta}\right)
\geq
\frac{1}{\mathcal{I}(\theta)}
=
\frac{1}
{
\mathrm{E}
\left[
\left[
\frac{\partial}{\partial \theta} \log f(X;\theta)
\right]^2
\right]
}](/pictures/eswiki/100/d67d8ff413670eb911477fab82d7b848.png)
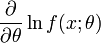
![\frac{\partial}{\partial\theta}
\left[
\int T(x) f(x;\theta) \,dx
\right]
=
\int T(x)
\left[
\frac{\partial}{\partial\theta} f(x;\theta)
\right]
\,dx](/pictures/eswiki/53/5cb7f5b7531809bf154687fe9a8d4d7b.png)
![\mathrm{var} \left(\widehat{\theta}\right)
\geq
\frac{1}{\mathcal{I}(\theta)}
=
\frac{1}
{
-\mathrm{E}
\left[
\frac{d^2}{d\theta^2} \log f(X;\theta)
\right]
}](/pictures/eswiki/52/498f244f1681ef9e7bd749a0c53bbf0f.png)
![\boldsymbol{\theta} = \left[ \theta_1, \theta_2, \dots, \theta_d \right]^T \in \mathbb{R}^d](/pictures/eswiki/97/a56e5028d90099485079fa761d07da68.png)
![\mathcal{I}_{m, k}
=
\mathrm{E}
\left[
\frac{d}{d\theta_m} \log f\left(x; \boldsymbol{\theta}\right)
\frac{d}{d\theta_k} \log f\left(x; \boldsymbol{\theta}\right)
\right]](/pictures/eswiki/52/4ea8a2257cb7235dc44bdd4d8faac8db.png)
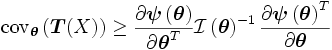
![\boldsymbol{\psi}
=
\mathrm{E}\left[\boldsymbol{T}(X)\right]
=
\begin{bmatrix} \psi_1\left(\boldsymbol{\theta}\right) &
\psi_2\left(\boldsymbol{\theta}\right) &
\cdots &
\psi_d\left(\boldsymbol{\theta}\right)
\end{bmatrix}^T](/pictures/eswiki/98/bcdc768d0e58b8370e5c4850a779234c.png)
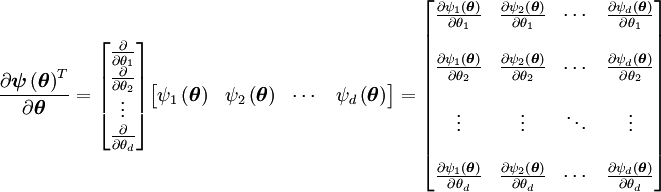
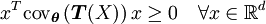
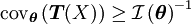
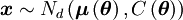
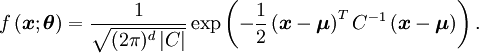
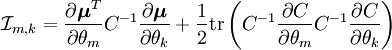
![w[n] \sim \mathbb{N}_N \left(\boldsymbol{\mu}(\theta), \sigma^2 {\mathcal I} \right).](/pictures/eswiki/52/4d780dcfaefcd02e8951eb7002923e9a.png)