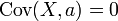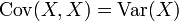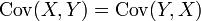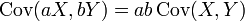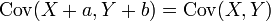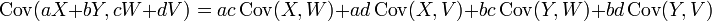- Covarianza
-
Covarianza
En estadística la covarianza es una medida de dispersión conjunta de dos variables estadísticas.
Definición
La covarianza S(X,Y) de dos variables aleatorias X e Y se define como:
- Si Sxy > 0 hay dependencia directa (positiva), es decir, a grandes valores de x corresponden grandes valores de y.
- Si Sxy = 0 Una covarianza 0 se interpreta como la no existencia de una relación lineal entre las dos variables estudiadas.
- Si Sxy < 0 hay dependencia inversa o negativa, es decir, a grandes valores de x corresponden pequeños valores de y.
La matriz de covarianza ΣXY de dos variables aleatorias n-dimensionales expresadas como vectores columna
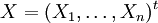 e
e 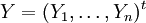 se define como:
se define como:donde
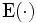 es el operador esperanza.
es el operador esperanza.Propiedades
- Si a todos los valores de la variable x, les sumamos una constante k y a todos los valores de la variable y, les sumamos una constante k’, la covarianza no varía.
- Si a todos los valores de una variable x los multiplicamos por una constante k y a todos los valores de la variable y, los multiplicamos por una constante k’, su covarianza queda multiplicada por el producto de las constantes.
- A partir de las anteriores: si tenemos dos variables x, y con la covarianza Sxy, y transformaciones lineales de las variables de la forma z=ax+b, y t=cy+d, la nueva covarianza se relaciona con la anterior de la forma: Szt = acSxy.
- Cov(x,y) = Cov(y,x)
Si X, Y, W, y V son variables aleatorias de valores reales y a, b, c, d son constantes ("constante" en este contexto significa no aleatorio), luego las siguientes verdades son consecuencia de la definición de covarianza:
Véase también
Categorías: Estadística descriptiva | Covarianza y correlación
Wikimedia foundation. 2010.

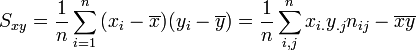
![S_{XY}={\operatorname{E}([X - \operatorname{E}(X)][Y - \operatorname{E}(Y)]^t)}](/pictures/eswiki/52/4c5cac26049f7927ad9fd7b44bfa155c.png)