- Criba de Eratóstenes
-
Criba de Eratóstenes
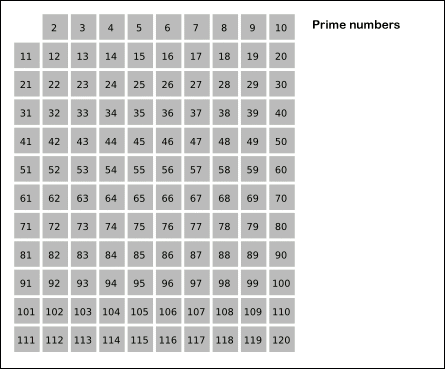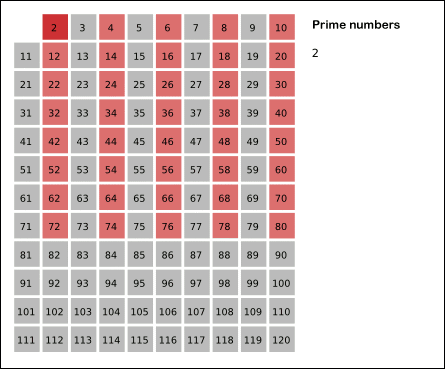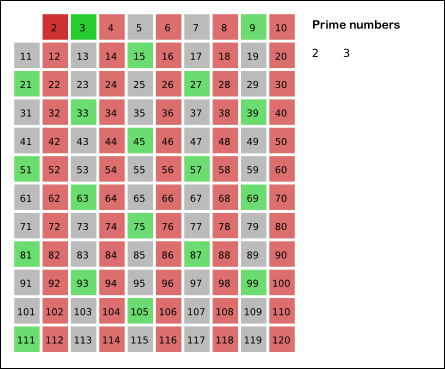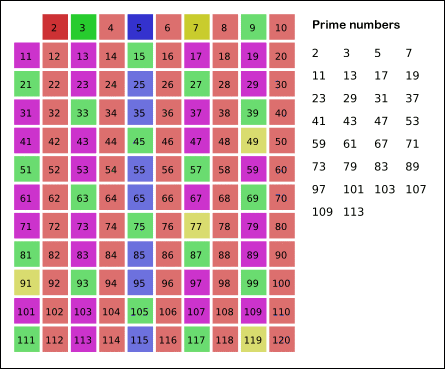
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado N. Se forma una tabla con todos los números naturales comprendidos entre 2 y N y se van tachando los números que no son primos de la siguiente manera: cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos. El proceso termina cuando el cuadrado del mayor número confirmado como primo es mayor que N.
Contenido
Pseudocódigo
Algoritmo Criba de Eratóstenes (Complejidad 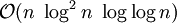 )
)Entrada: Un número natural n
Salida: El conjunto de números primos anteriores a n (incluyendo n)
- Escriba todos los números naturales desde 2 hasta n
- Para i desde 2 hasta
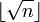 haga lo siguiente:
haga lo siguiente:
- Si i no ha sido marcado entonces:
- Para j desde i hasta
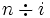 haga lo siguiente:
haga lo siguiente:
- Ponga una marca en
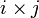
- Ponga una marca en
- Para j desde i hasta
- Si i no ha sido marcado entonces:
- El resultado es: Todos los números sin marca
Acerca de la notación:
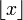 es la función parte entera de x
es la función parte entera de x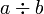 es el cociente de dividir a entre b
es el cociente de dividir a entre b
Para su implementación en una computadora, normalmente se maneja un vector de tipo lógico con n elementos. De esta manera, la posición i contiene el valor Verdadero como representación de que i ha sido marcado y Falso en otro caso.
Implementacion
En lenguaje Python
#Criba de Erastostenes por Calvo from math import sqrt,floor n=float(raw_input('Introduzca un valor N: ')) d={} p=2, for i in range(2,floor(sqrt(n))+1): if i not in d.keys(): for j in range(i,n/i+1): d[i*j]=1 for i in range(n,1,-1): if i not in d.keys(): print i
En Lenguaje de programación Ada
procedure Eratosthenes(Result : out Integer) is size : constant := 8190; k, prime : Natural; count : Integer; type Ftype is array (0 .. Size) of Boolean; Flags : Ftype; begin for Iter in 1 .. 10 loop count := 0; for i in 0 .. size loop Flags (i) := True; end loop; for i in 0 .. size loop if Flags (i) then prime := i + i + 3; k := i + prime; while k <= size loop Flags (k) := False; k := k + prime; end loop; count := count + 1; end if; end loop; end loop; Result := count; end Eratosthenes;
En lenguaje Basic
defint a-z size=50 dim flags(50) for i=2 to size flags(i)=-1 next for i=2 to sqr(size) if flags(i) then for k=i*i to size step i flags(k)=0 next end if next for i=0 to size if flags(i) then print i; next print
En lenguaje Bash
#!/bin/bash UPPER_LIMIT=$1 let SPLIT=UPPER_LIMIT/2 Primes=( '' $(seq $UPPER_LIMIT) ) i=1 until (( ( i += 1 ) > SPLIT )) do if [[ -n $Primes[i] ]] then t=$i until (( ( t += i ) > UPPER_LIMIT )) do Primes[t]= done fi done echo ${Primes[*]} exit 0
/* Sieve Of Erathosthenes by Denis Sureau */ #include <stdlib.h> #include <stdio.h> void eratosthenes(int top) { int all[10000]; int idx = 0; int prime = 3; int x, j; printf("1 "); while(prime <= top) { for(x = 0; x < top; x++) { if(all[x] == prime) goto skip; } printf("%d ", prime); j = prime; while(j <= (top / prime)) { all[idx++] = prime * j; j += 1; } skip: prime+=2; } puts(""); return; } int main(int argc, char **argv) { if(argc == 2) eratosthenes(atoi(argv[1])); else eratosthenes(50); return 0; }
En lenguaje C++
#include <iostream> using namespace std; void criba(bool* & m, int tam){ m = new bool[tam + 1]; m[0] = false; for(int i = 1; i <= tam; ++i) m[i] = true; for(int i = 2; i*i <= tam; ++i) if(m[i]) for(int h = 2; i*h <= tam; ++h) m[i*h] = false; } int main(void){ int tope; bool* m_criba; cout << "Ingrese el tope de la criba: "; cin >> tope; criba(m_criba, tope); for(int i = 2; i <= tope; ++i) if(m_criba[i]) cout << i << ' '; cout << endl; delete [] m_criba; fflush(stdin); getchar(); }
En lenguaje Fortran
* Sieve of Eratosthenes by Chuck Bouldin top = 50 logical*2 flags(top) integer*2 i,j,k,count,iter,prime n = long(362) do 92 iter = 1,10 count=0 i=0 do 10 i = 1,top 10 flags(i) = .true. do 91 i = 1,top if (.not. flags(i)) go to 91 prime = i + i + 3 count = count + 1 k = i + prime if (k .gt. top) go to 91 do 60 j = k, top, prime 60 flags(j) = .false. 91 continue 92 continue write (9,*) count," primes in ",(long(362)-n)/60.0," seconds " pause end
En Lenguaje de programación Java
public class Eratosthenes { public static void main(String[] args) { int N = Integer.parseInt(args[0]); boolean[] isPrime = new boolean[N + 1]; for (int i = 2; i <= N; i++) isPrime[i] = true; for (int i = 2; i*i <= N; i++) { if (isPrime[i]) { for (int j = i; i*j <= N; j++) isPrime[i*j] = false; } } int primes = 0; for (int i = 2; i <= N; i++) { if (isPrime[i]) System.out.println(" " + i); } } }
En Lenguaje de programación Pascal
program Eratosthenes; const N=1000; var a:ARRAY[1..N] of boolean; i,j,m:word; begin for i:=1 TO N do A[i]:=TRUE; m:=trunc(sqrt(N)); for i:=2 to m do if a[i] then for j:=2 to N DIV i do a[i*j]:=FALSE; for i:=1 to N do if a[i] then write(i:4); end.
En lenguaje Perl
#!/usr/bin/perl $n = 50; for ( $i=1; $i<=$n; $i++ ) { $p[$i] = $i; } $k = int( sqrt($n) ); $i=2; while ( $i <= $k ) { while ( $p[ $i ] == 0 ) { $i ++; } for ( $j=2; $j<=$n; $j++ ) { $a = $i * $j; $p[ $a ] = 0; } $i++; } for ( $i=1; $i<=$n; $i++ ) { if ( $p[$i] != 0 ) { printf ( "%d\n", $p[$i] ); } }
En lenguaje PHP
<?php /* Sieve Of Erathosthenes by Denis Sureau */ function eratosthenes($n) { $all=array(); $prime=1; echo 1," ",2; $i=3; while($i<=$n) { if(!in_array($i,$all)) { echo " ",$i; $prime+=1; $j=$i; while($j<=($n/$i)) { array_push($all,$i*$j); $j+=1; } } $i+=2; } echo "\n"; return; } eratosthenes(50); ?>
En lenguaje Ruby
# sieve of Eratosthenes from the ruby distro top = Integer(ARGV.shift || 100) sieve = [] for i in 2 .. top sieve[i] = i end for i in 2 .. Math.sqrt(top) next unless sieve[i] (i*i).step(top, i) do |j| sieve[j] = nil end end puts sieve.compact.join " "
En lenguaje Visual Basic .NET
Module Eratosthenes 'Sieve of Eratosthenes by Marcelo Rivera Sub Main() Dim number As Integer number = 20 Dim IsPrime(number) As Boolean For i As Integer = 2 To number If IsPrime(i - 1) = False Then For j As Integer = i To number / i IsPrime((i * j) - 1) = True Next End If Next For x As Integer = 1 To number - 1 If IsPrime(x) = False Then Console.WriteLine(x + 1) End If Next End Sub End ModuleRefinamiento
Una implementación más eficiente requiere crear un arreglo con solo los impares (pues los pares distintos de 2 ya se sabe que no son primos). En este caso se deben tachar los múltiplos impares de 3,4,5,6...
Los múltiplos impares del primo p = 2i + 3 son (2k + 1)(2i + 3). Debemos tachar desde k = i + 1 en adelante pues siempre se empieza a tachar desde p2. Note que si k = i + 1 entonces el primer múltiplo de p = 2i + 3 es (2k + 1)(2i + 3) = p2.
Si corresponde tachar los múltiplos del primo k − ésimo pk, se inicia en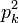 pues antes de pk, ya se han tachado 2pk (los pares), 3pk (los múltiplos de 3), 5pk,...,
pues antes de pk, ya se han tachado 2pk (los pares), 3pk (los múltiplos de 3), 5pk,...,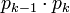 .
.Así, si
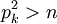 ya no habría algo que tachar, por eso terminamos ahí el programa.
ya no habría algo que tachar, por eso terminamos ahí el programa.
En la implementación se usa un arreglo "esPrimo()" tipo boolean. Aquí, "esPrimo(i)" representa al número impar 2i + 3.
Note que si p = 2i + 3 entonces p está representado por "esPrimo((p-3)/2)".
Así, si se sabe que p = 2i + 3 es primo, sus múltiplos (impares) no son primos, es decir, debemos poner"esPrimo(((2k+1)p-3)/2)=false, k=i+1,i+2,..."
En la implementación iniciamos con el arreglo "esPrimo()" con todas sus entradas true. Iniciando en p = 3, ponemos "esPrimo(((2k+1)3-3)/2)=false, k=0+1,0+2,..." y así sucesivamente: para cada nuevo i primero preguntamos si "esPrimo(i)=true", si es así, "tachamos" sus múltiplos poniendo la respectiva entrada "false".
La siguiente función, en VBA, es una función que recibe n y devuelve un arreglo con los primos
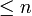 (ver más detalles en la segunda referencia)
(ver más detalles en la segunda referencia)Function ERATOSTENES(n) As Long() Dim i, j, k, pos, contaPrimos Dim max As Long Dim esPrimo() As Boolean Dim Primos() As Long max = (n - 3) \ 2 ' División entera ReDim esPrimo(max + 1) ReDim Primos(max + 1) For i = 0 To max esPrimo(i) = True Next i contaPrimos = 0 Primos(0) = 2 'contado el 2 j = 0 While (2 * j + 3) <= n\(2 * j + 3) k = j + 1 If esPrimo(j) Then While (2 * k + 1) <= n\(2 * j + 3) pos = ((2 * k + 1) * (2 * j + 3) - 3) \ 2 esPrimo(pos) = False k = k + 1 Wend End If j = j + 1 Wend For i = 0 To max If esPrimo(i) Then contaPrimos = contaPrimos + 1 '3,5,... Primos(contaPrimos) = 2 * i + 3 End If Next i ReDim Preserve Primos(contaPrimos) 'Cortamos el vector ERATOSTENES = Primos() End Function
En Lenguaje de Programación Java
import javax.swing.JOptionPane; public class Erastostenes { public static void main( String args[] ) { // Contribución de David Jesús ( UNMSM - FISI ) int N = Integer.parseInt( JOptionPane.showInputDialog( "Limite superior :" ) ); int k, pos; int numMaxPrimos = ( N - 3 ) / 2 ; int numPrimos = 0; int[] Primos = new int[ numMaxPrimos + 1 ]; boolean[] esPrimo = new boolean[ numMaxPrimos + 1 ]; for( int i = 0; i < numMaxPrimos; i ++ ) esPrimo[ i ] = true; for( int i = 0; i*i < N; i ++ ) { k = i + 1; if( esPrimo[ i ] ) { for( k = i + 1; ( 2 * k + 1 ) * ( 2 * i + 3 ) <= N; k ++ ) { pos = ( ( 2 * k + 1 ) * ( 2 * i + 3 ) - 3 ) / 2; esPrimo[ pos ] = false; } } } // Mostramos y a la vez guardamos los numeros primos en el vector Primos[ 0 ] = 2; System.out.print( " 2" ); for( int i = 0; i <= numMaxPrimos; i ++ ) { if( esPrimo[ i ] ) { numPrimos ++; Primos[ numPrimos ] = 2 * i + 3; System.out.print( " " + Primos[ numPrimos ] ); } } } }
Véase también
Referencias
- Samuel Horsley (1772). «KOΣKINON EPATOΣΘENOΥΣ. or, The Sieve of Eratosthenes. Being an Account of His Method of Finding All the Prime Numbers, by the Rev. Samuel Horsley, F. R. S.» Philosophical Transactions (1683-1775). Vol. 62.
- Walter Mora F. «Criba de Eratóstenes» Revista digital Matemática: Educación e Internet. Vol. 7. n.º 2.
Categorías: Tests de primalidad | Teoría de cribas
Wikimedia foundation. 2010.
