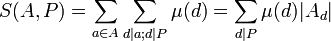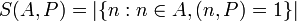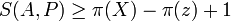- Criba de Legendre
-
Criba de Legendre
En matemáticas, la criba de Legendre es el más simple método en teoría de cribas. Este aplica el concepto de la criba de Eratostenes para encontrar estimativos superiores e inferiores al número de primos en un conjunto de enteros dado. Debido a que este es una extensión simple de la idea usada en la criba de Eratostenes, este método de cribado es llamado algunas veces la criba de Eratostenes-Legendre.
Identidad de Legendre
La idea central del método es expresada por la siguiente identidad, algunas veces llamada la Identidad de Legendre:
Donde A es un conjunto de enteros, P es un producto de distintos primos, μ es la función de Möbius, Ad es el conjunto de enteros en A divisible por d, y S(A, P) es definido como:
Luego S(A,P) es la cantidad de números en A sin factores comunes con P.
Note que en el caso más típico, A es el conjunto de todos los enteros menores o iguales a un número real X, P es el producto de todos los primos menores o iguales a algún entero z < X, asumiendo esto, la identidad de Legendre tomaría la forma:
S(A,P)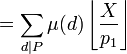 
![=[X] - \sum_{p_1 < z} \left\lfloor\frac{X}{p_1}\right\rfloor + \sum_{p_1 < p_2 < z}
\left\lfloor\frac{X}{p_1p_2}\right\rfloor - \sum_{p_1 < p_2 < p_3 < z}
\left\lfloor\frac{X}{p_1p_2p_3}\right\rfloor + \cdots](/pictures/eswiki/57/9f229a6e29434ed39a63b0f3c36717ec.png)
(donde
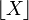denota la función parte entera). En este ejemplo, el hecho de que la criba de Legendre se derive de la criba de Eratostenes es claro: el primer término es el número de interos menores que X, el segundo término remueve los múltiplos de todos los primos, el tercero añade los múltiplos de dos primos (los cuales fueron descontados por que se "tacharon dos veces"), y así de manera sucesiva todos las 2π(z) (donde π(z) denota el número de primos menores que z) combinaciones de primos son consideradas por la criba de Legendre.Una vez se ha calculado S(A,P) para este caso especial, este puede ser usado para acotar π(X) usando la expresión
la cual es una implicación clara de la definición de S(A,P).
Problemas
Desafortunadamente, la criba de Legendre tiene un problema con la parte fraccionaria de los diferentes términos, los cuales se acumulan en un término de error (esto es, términos en notación O) demasiado grande, la cual dice que la criba de Legendre da cotas muy débiles en muchos casos. Por esta razón, esta criba nunca es usada en la práctica, siendo siempre mejorada por otras técnicas de cribado tales como la Criba de Brun y la Criba de Selberg. Sin embargo, dado que estas cribas más poderosas son extensiones de las ideas básicas de la criba de Legendre, este método de cribado se vuelve util para entender cómo trabajan las cribas.
Véase
Categorías: Teoría analítica de números | Teoría de cribas
Wikimedia foundation. 2010.
