Función de Möbius

Función de Möbius

La función de Möbius μ(n), nombrada así en honor a August Ferdinand Möbius, es una función multiplicativa estudiada en teoría de números y en combinatoria.

Contenido

Definición

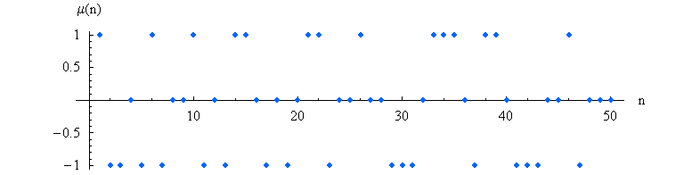
μ(n) está definida para todos los números naturales n y tiene valores en {-1, 0, 1} dependiendo en la factorización de n en sus factores primos. Se define como sigue:

  • μ(n) = 1 si n es libre de cuadrados y tiene un número par de factores primos distintos.
  • μ(n) = -1 si n es libre de cuadrados y tiene un número impar de factores primos distintos.
  • μ(n) = 0 si n es divisible por algún cuadrado.

Una definición equivalente se define haciendo uso de las funciones ω(n) y Ω(n), donde:

  • ω(n) obtiene el número de primos distintos que dividen el número.
  • Ω(n) obtiene el número de factores primos de n, incluyendo sus multiplicidades. Claramente, ω(n) ≤ Ω(n).

Así, se define la función de Möbius como

\mu(n)= \begin{cases} (-1)^{\omega(n)}=(-1)^{\Omega(n)} &\mbox{si }\; \omega(n) = \Omega(n)\\ 0&\mbox{si }\;\omega(n) < \Omega(n). \end{cases}

La definición implica que μ(1) = 1, ya que 1 tiene 0 factores primos distintos, por lo tanto, un número par.

los 50 primeros valores de la función μ(n).

Propiedades y aplicaciones

La función de Möbius es multiplicativa, y tiene gran relevancia en la teoría de las funciones multiplicativas y aritméticas puesto que aparece en la fórmula de inversión de Möbius. La suma sobre todos los divisores positivos de n de la función de Möbius es cero excepto cuando n = 1.

\sum_{d | n} \mu(d) = \begin{cases}1&\mbox{ si } n=1\\ 0&\mbox{ si } n>1. \end{cases}

Otras aplicaciones de μ(n) en combinatoria están relacionadas con el uso del teorema de Pólya en grupos combinatorios.

Teoría de números

Artículo principal: función de Mertens

En teoría de números, la función de Mertens está emparentada con la función de Möbius, y se define como:

M(n) = \sum_{1\le k \le n} \mu(k)

para todo número natural n.
Esta función está relacionada con las posiciones de los ceros de la función ζ de Euler-Riemann y con la conjetura de Riemann.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Función de Möbius — La función de Möbius µ(n), nombrada así en honor a August Ferdinand Möbius, es una función multiplicativa estudiada en teoría de números y en combinatoria …   Enciclopedia Universal

  • Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje …   Wikipedia Español

  • Función φ de Euler — Los primeros mil valores de . La función φ de Euler (también llamada función indicatriz de Euler) es una función importante en teoría de números. Si n es un número entero positivo, entonces φ(n) se define como el número de enteros positivos… …   Wikipedia Español

  • Función de Mertens — En teoría de números, la función de Mertens se define como: donde μ(k) es la función de Möbius. Dado que la función de Möbius contempla solo las imágenes { 1,0,1} resulta obvio que la función de Mertens apenas varía en su recorrido y que no… …   Wikipedia Español

  • Función multiplicativa — En teoría de números, una función discreta (es decir, definida para n entero) se dice multiplicativa si f(1) = 1 f(m·n) = f(m)·f(n) cuando m y n son enteros coprimos (no tienen factores comunes). Una función multiplicativa queda determinada si se …   Wikipedia Español

  • Función de Mertens — En teoría de números, la función de Mertens se define como: donde µ(k) es lae función de Möbius. Algunos valores de la función de Mertens se encuentran en SIDN A002321 …   Enciclopedia Universal

  • Función zeta prima — En matemática, la función zeta prima es un análogo de la función zeta de Riemann, estudiada por Glaisher (1891). Está definida por la siguiente serie infinita, la cual converge para todo : . El producto de Euler para la función zeta de… …   Wikipedia Español

  • Fórmula de inversión de Möbius — La clásica fórmula de inversión de Möbius fue introducida en la teoría de números durante el siglo XIX por August Ferdinand Möbius. Fue generalizada más adelante a otras fórmulas de inversión de Möbius . Formulación La versión clásica establece… …   Wikipedia Español

  • Transformación de Möbius — En geometría, una transformación de Möbius es una función de la forma: donde z, a, b, c, d son números complejos que verifican que ad − bc ≠ 0. Una transformación de Möbius puede verse en el plano complejo como la composición de una proyección… …   Wikipedia Español

  • August Möbius — Saltar a navegación, búsqueda August Möbius August Ferdinand Möbius (17 de noviembre de 1790, Schulpforta, Sajonia, Alemania 26 de septiembre de 1868, Leipzig …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”