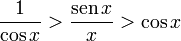Teorema del sándwich

Teorema del sándwich

Teorema del sándwich

En cálculo, el teorema del sándwich (llamado también teorema de encaje, teorema de intercalación, teorema del enclaustramiento, teorema de compresión,teorema de las funciones mayorante y minorante, criterio del sándwich, teorema del emparedado o squeeze theorem en inglés) es un teorema usado en la determinación del límite de una función. Este teorema enuncia que si dos funciones tienden al mismo límite en un punto, cualquier otra función que pueda ser acotada entre las dos anteriores tendrá el mismo límite en el punto.

El teorema o criterio del sándwich es muy importante en demostraciones de cálculo y análisis matemático. Y es frecuentemente utilizado para encontrar el límite de una función a través de la comparación con otras dos funciones de límite conocido o fácilmente calculable. Fue utilizado por primera vez de forma geométrica por Arquímedes y Eudoxo en sus esfuerzos por calcular π. Aunque la formulación moderna fue obra de Gauss.

Contenido

Exposición

El teorema del encaje o de intercalación es expuesto formalmente como:

Sea I un entorno del punto a. Y sean f, g y h funciones definidas en I, exceptuando quizás el mismo punto a. Supongamos que para todo x en I diferente de a tenemos:

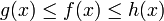
g(x) \leq f(x) \leq h(x)

y supongamos también que:

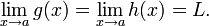
\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L.

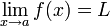Entonces \lim_{x \to a} f(x) = L.


  • Las funciones g(x) y h(x) son llamadas cotas de f(x), o también funciones minorante y mayorante de f(x) respectivamente.

Indeterminaciones

Uno de los usos más frecuentes del teorema del sándwich es en la resolución de límites indeterminados. En particular, permite afirmar que el límite 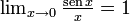\textstyle \lim_{x\to 0} \frac{\operatorname{sen\,} x}{x} = 1. Algunas indeterminaciones pueden resolverse despejando dicha expresión de la expresión general y aplicando propiedades del límite con el resto.

Demostración

Se intenta calcular el límite 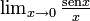\textstyle \lim_{x\to 0} \frac{\operatorname{sen} x}{x}, que es una indeterminación del tipo \frac{0}{0}.

  • Se toma la relación 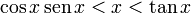\cos x \, \operatorname{sen\,} x < x < \tan x en el intervalo (0,π/2).
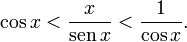
  • Haciendo algunas operaciones resulta en \cos x < \frac{x}{\operatorname{sen\,} x} < \frac{1}{\cos x}.
  • \frac{1}{\cos x} > \frac{\operatorname{sen\,} x}{x} > \cos x
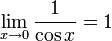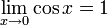
  • Se sabe que \lim_{x\to 0} \frac{1}{\cos x} = 1 y que \lim_{x\to 0} \cos x = 1
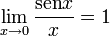  • Por el teorema de sandwich, \lim_{x\to 0} \frac{\operatorname{sen} x}{x} = 1.

Referencias

Véase también

Obtenido de "Teorema del s%C3%A1ndwich"

Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Teorema del sándwich de jamón — Para el teorema sobre el límite de una función comprendida entre otras, ver Teorema del sándwich En la teoría de la medida, una rama de las matemáticas, el Teorema del sandwich de jamón (Ham sandwich theorem), también llamado Teorema de Stone… …   Wikipedia Español

  • Teorema del emparedado — En cálculo, el teorema del emparedado (llamado también teorema de encaje, teorema de intercalación, teorema de estricción, teorema del enclaustramiento, teorema de compresión,teorema de las funciones mayorante y minorante, criterio del sándwich,… …   Wikipedia Español

  • Sándwich (desambiguación) — Sándwich puede hacer referencia a: Al sándwich o emparedado, una comida preparada por dos mitades de panes (o dos rebanadas) que cubren un relleno. Véase también Categoría:Sándwiches. Contenido 1 Ciudades 2 Isla 3 Puerto …   Wikipedia Español

  • Sándwich de jamón — Una variedad de sándwich de jamón tipo sub . El sándwich de jamón o emparedado de jamón es un tipo de sándwich muy común. Se prepara colocando el jamón cortado entre dos rebanadas de pan.[1] …   Wikipedia Español

  • Límite de una función — El límite de una función es un concepto fundamental del cálculo diferencial matemático, un caso de límite aplicado a las funciones. Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser… …   Wikipedia Español

  • Derivación de funciones trigonométricas — Saltar a navegación, búsqueda Función Derivada sin(x) cos(x) cos(x) − sin(x) tan(x) sec2(x) …   Wikipedia Español

  • Hiperplano — En geometría, un hiperplano es una generalización del concepto de plano. En un espacio unidimensional (como una recta), un hiperplano es un punto; divide una línea en dos líneas. En un espacio bidimensional (como el plano xy), un hiperplano es… …   Wikipedia Español

  • Problema de Basilea — Saltar a navegación, búsqueda El Problema de Basilea es un famoso problema de teoría de números, planteado por primera vez por Pietro Mengoli, y resuelto por Leonhard Euler en 1735. Puesto que el problema había resistido los ataques de los… …   Wikipedia Español

  • Espacio de Hilbert equipado — Saltar a navegación, búsqueda En matemáticas, un espacio de Hilbert equipado (EHE) es una generalización de los espacios de Hilbert que permite ligar la teoría de distribuciones y los aspectos cuadrado integrables del análisis funcional. Tales… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”