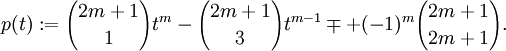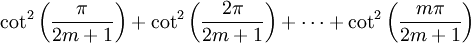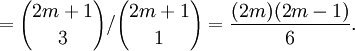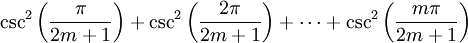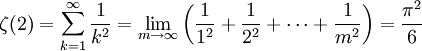- Problema de Basilea
-
Problema de Basilea
El Problema de Basilea es un famoso problema de teoría de números, planteado por primera vez por Pietro Mengoli, y resuelto por Leonhard Euler en 1735. Puesto que el problema había resistido los ataques de los matemáticos más importantes de la época, la solución llevó a Euler rápidamente a la fama cuando tenía veintiocho años. Euler generalizó el problema considerablemente, y sus ideas fueron tomadas años después por Bernhard Riemann en su artículo de 1859 On the Number of Primes Less Than a Given Magnitude, en donde definió su función zeta y demostró sus propiedades básicas. El problema debe su nombre a la ciudad de residencia de Euler (Basilea), ciudad donde vivía también la familia Bernoulli, que atacó el problema sin éxito.
El problema de Basilea consiste en encontrar la suma exacta de los inversos de los cuadrados de los enteros positivos, esto es, la suma exacta de la serie infinita:
Numéricamente, se puede obtener que la serie es aproximadamente igual a 1,644934. Sin embargo, el problema de Basilea busca la suma exacta de la serie, de forma cerrada, así como una demostración de que dicha suma es correcta. Euler encontró que la suma exacta era π2/6 y anunció su descubrimiento en 1735. Sus argumentos estaban basados en manipulaciones que no estaban aun justificadas, y no fue hasta 1741 cuando pudo dar una demostración verdaderamente rigurosa.
Aunque es poco conocido, esta suma puede escribirse, de manera integral, como función de dos variables. A menudo, se coloca como ejercicio para los estudiantes de matemáticas:
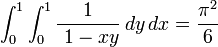
Contenido
Euler ataca el problema
El método inicial de Euler para la obtención del valor π2/6 es original e ingenioso. En esencia, lo que hizo fue extender resultados aplicables a polinomios finitos, considerándolos también válidos para series infinitas. Claro está que el razonamiento de Euler requiere justificación, pero aun sin ella, simplemente obteniendo el valor correcto, pudo verificarlo numéricamente frente a sumas parciales de la serie. La concordancia observada le dio suficiente confianza como para anunciar su resultado a la comunidad matemática.
Para seguir el razonamiento de Euler, hay que recordar el desarrollo en serie de Taylor de la función seno:
Dividiendo por x, tenemos
Ahora bien, las raíces (ceros) de sin(x)/x se encuentran precisamente en
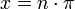 , donde n = ±1, ±2, ±3... Asumamos que podemos expresar esta serie infinita como producto de factores lineales dados por las raíces, de la misma forma que hacemos con los polinomios finitos:
, donde n = ±1, ±2, ±3... Asumamos que podemos expresar esta serie infinita como producto de factores lineales dados por las raíces, de la misma forma que hacemos con los polinomios finitos:Si hacemos este producto y agrupamos todos los términos en x2, vemos que el coeficiente de x2 para la función sin(x)/x es
Pero del desarrollo en serie de Taylor original de sin(x)/x, tenemos que el coeficiente de x2 es −1/(3!) = −1/6. Estos dos coeficientes deben ser iguales (por el teorema de unicidad del desarrollo en serie); por tanto,
Multiplicando ambos miembros de la igualdad por −π2 obtenemos la suma de los inversos de los cuadrados de los enteros positivos.
La función zeta de Riemann
La función zeta de Riemann ζ(s) es una de las funciones más importantes en matemáticas, debido a su relación con la distribución de los números primos. La función está definida para todo número complejo s cuya parte real sea mayor que la unidad (Re(s) > 1) por la siguiente fórmula:
Haciendo s = 2, vemos que ζ(2) es igual a la suma de los inversos de los cuadrados de los enteros positivos.
¿Cómo sabemos que la suma converge? Podemos demostrarlo con la siguiente desigualdad:
Esto marca el límite superior ζ(2) < 2, y como la suma infinita tiene sólo términos positivos, debe converger. Puede demostrarse que ζ(s) se expresa en términos de los números de Bernoulli siempre que s sea un número par positivo.
Una demostración rigurosa
El siguiente razonamiento demuestra la identidad ζ(2) = π2/6, donde ζ(s) es la función zeta de Riemann. Es con mucho la demostración más sencilla hasta ahora disponible; mientras otras demostraciones emplean resultados de matemática avanzada, como análisis de Fourier, análisis complejo, y cálculo multivariable, la siguiente no requiere siquiera cálculo de una variable (aunque es necesaria la obtención de un límite al final).
Historia de la demostración
El origen de la demostración es incierto. Apareció en la revista Eureka en 1982, atribuida a John Scholes, pero Scholes dice haber aprendido la demostración de Peter Swinnerton-Dyer, y en cualquier caso mantiene que ésta era "de dominio público en la Universidad de Cambridge a finales de los 60".
Lo que se necesita saber
Para comprender la demostración, es necesario conocer los siguientes resultados:
- La fórmula de De Moivre establece que, para todo número real x y para todo número entero n,
- Demostración: se puede demostrar a partir de la fórmula de Euler.
- El binomio de Newton, que establece que para cualquier par de números reales x e y y cualquier número natural n,
- donde los coeficientes binomiales son
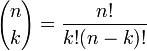 (ver factorial)
(ver factorial)
- Demostración: se necesitan inducción matemática y algunas propiedades de los coeficientes binomiales.
- La función cot2 x es inyectiva en el intervalo (0, π/2).
- Demostración: supongamos cot2 x = cot2 y para algún x y algún y en el intervalo (0, π/2). Usando la definición de cotangente cot x = (cos x)/(sin x) y la identidad trigonométrica cos2 x = 1 − sin2 x, vemos que (sin2 x)(1 − sin2 y) = (sin2 y)(1 − sin2 x). Restando (sin2 x)(sin2 y) a cada miembro, tenemos sin2 x = sin2 y. Dado que la función seno es no negativa en el intervalo (0, π/2), esto significa que sin x = sin y, pero es geométricamente evidente (observando el círculo unidad, por ejemplo) que la función seno es inyectiva en el intervalo (0, π/2), por lo que x = y, como queríamos demostrar.
- Si p(t) es un polinomio de grado m, entonces p no tiene más de m raíces distintas.
- Demostración: es una consecuencia del teorema fundamental del álgebra.
- Si p(t) = amtm + am − 1tm − 1 +... + a1t + a0, donde am ≠ 0, entonces la suma de las raíces de p (contando la múltiples) es −am − 1/am.
- Demostración: Si am = 1, entonces p(t) = ∏(t − s), donde s abarca todas las raíces de p. Desarrollando este producto, vemos que el coeficiente de tm − 1 es menos la suma de todas las raíces. Si am ≠ 1, podemos dividir cada término por este valor, obteniendo un nuevo polinomio con las mismas raíces, cuyo coeficiente principal es ahora 1; aplicando el razonamiento precedente vemos que la suma de las raíces del polinomio original p(t) = suma de las raíces del nuevo polinomio = −am − 1/am.
- La identidad trigonométrica csc2 x = 1 + cot2 x.
- Demostración: se sigue de la identidad fundamental 1 = sin2 x + cos2 x tras dividir ambos miembros por sin2 x.
- Para todo número real x siendo 0 < x < π/2, se cumplen las desigualdades cot2 x < 1/x2 < csc2 x.
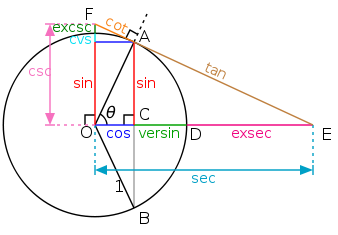
- Demostración: fijémonos primero en que 0 < sin x < x < tan x. Esto puede verse en el siguiente esquema:
- Para ver que 0 < sin x < x, hay que observar que en el dibujo, sin θ es la longitud del segmento AC, y θ la longitud del arco AD.
- Para ver que x < tan x, obsérvese que el área del triángulo OAE es tan(θ)/2, el área del sector OAD es θ/2, y que el sector está contenido en el triángulo.
- Ahora, tomemos los inversos y elevemos al cuadrado en las desigualdades, recordando que éstas deben cambiar el sentido. Obtenemos así las desigualdades buscadas.
- Otra demostración, menos geométrica, puede conseguirse con: sea f(x) = sin x - x, vemos que f(0) = 0 y f'(x) = cos x - 1 < 0 (en casi todo punto), lo que implica que f es estrictamente decreciente, deduciendo que f(x) < 0 y, por tanto, que sin x < x.
- Para ver la otra desigualdad, definimos g(x) = tan x - x y aplicamos el mismo razonamiento.
- Sean a, b, y c números reales, con a y c no nulos; entonces el límite de la función (am + b)/(am + c) cuando m tiende a infinito es 1.
- Demostración: dividamos cada término por m, obteniendo (a + b/m)/(a + c/m). Si dividimos un número fijo por un número cada vez mayor, el cociente se aproxima a cero; por tanto, tanto el numerador como el denominador tienden a a, por lo que su cociente tenderá a 1.
- El criterio del sandwich, que establece que si una función se encuentra acotada entre otras dos funciones, y estas dos funciones tienden ambas a un mismo límite, entonces la función acotada por ellas tiende igualmente a dicho límite.
- Demostración: ver el artículo squeeze theorem (en inglés) para una discusión y demostración detalladas.
La demostración
La idea principal en la que descansa la demostración es la de limitar las sumas parciales
entre dos expresiones, las cuales tenderán ambas a π2/6 cuando m tienda a infinito. Las dos expresiones se obtienen de identidades que incluyen las funciones cotangente y cosecante. Estas identidades son a su vez obtenidas de la fórmula de De Moivre, y eso es lo que nos disponemos a hacer ahora.
Sea x un número real tal que 0 < x < π/2, y sea n un entero positivo. Entonces de la fórmula de De Moivre y de la definición de cotangente, tenemos
Del binomio de Newton, tenemos
Combinando ambas ecuaciones e igualando las partes imaginarias, obtenemos la identidad
Tomamos esta identidad y establecemos que n = 2m + 1, siendo m un entero positivo, y x = r π/(2m + 1), siendo r = 1, 2,..., m. Entonces nx = r π, por lo que sin(nx) = 0 y, de esta forma,
Esta ecuación es válida para todos los valores de x = r π/(2m + 1), tales que r = 1, 2,..., m. Estos valores de x son números distintos estrictamente entre 0 y π/2. Dado que la función cot2(x) es inyectiva en el intervalo (0, π/2), los números cot2(x) = cot2(r π/(2m + 1)) son distintos para cada valor de r = 1, 2,..., m. Pero por la ecuación anterior, cada uno de estos m números distintos es una raíz del polinomio de grado m
Esto significa que los números x = cot2(r π/(2m + 1)), para r = 1, 2,..., m son precisamente las raíces del polinomio p(t). Pero podemos calcular directamente la suma de las raíces examinando los coeficientes, y la comparación muestra que
Sustituyendo la identidad csc2 x = cot2 x + 1, tenemos
Consideremos ahora la desigualdad cot2 x < 1/x2 < csc2 x. Si sumamos todas estas desigualdades para cada uno de los valores x = r π/(2m + 1), y empleamos las dos identidades anteriores, obtenemos
Multiplicando todo por (π/(2m + 1))2, pasamos a
Cuando m tiende a infinito, las expresiones a la izquierda y a la derecha tienden ambas a π2/6, luego por el criterio del sandwich,
con lo que queda completa la demostración. C.Q.D.
Aplicación al cálculo de π
En 1881, Ernesto Cesaro demostró que la probabilidad de que dos enteros sean primos relativos es 6 / π2, que es el inverso de ζ(2). Mediante la demostración de más arriba, el teorema de Cesaro permite calcular un valor para π a partir de una muestra grande de enteros aleatorios, determinando la proporción de éstos que son primos relativos.
Referencias
- Number Theory: An Approach Through History, Andre Weil, Springer, ISBN 0-8176-3141-0
- Euler: The Master of Us All, William Dunham, MAA, ISBN 0-88385-328-0
- Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics, John Derbyshire, Joseph Henry Press, ISBN 0-309-08549-7
- Proofs From the Book, Martin Aigner, Gunter Ziegler, Springer, ISBN 3-540-67865-4
- Riemann's Zeta Function, Harold M. Edwards, Dover, ISBN 0-486-41740-9
Enlaces externos
- Euler's solution of the Basel problem -- the longer story
- How Euler did it
- The infinite series of Euler and the Bernoulli's spice up a calculus class
- Fourteen proofs of the evaluation of ζ(2), compiled by Robin Chapman
Categoría: Teoría de números
Wikimedia foundation. 2010.

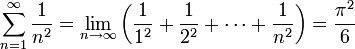
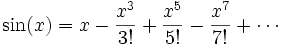
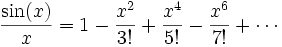
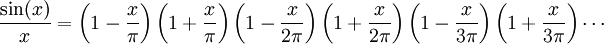
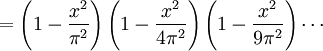
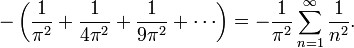
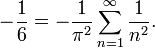
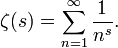
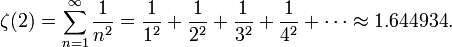
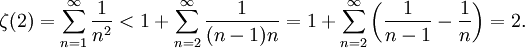
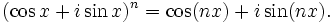

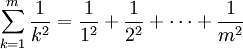
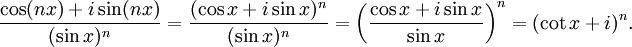
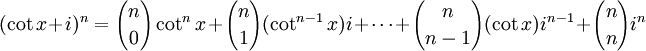
![= \left[ {n \choose 0} \cot^n x - {n \choose 2} \cot^{n-2} x \pm \cdots \right] \; + \; i\left[ {n \choose 1} \cot^{n-1} x - {n \choose 3} \cot^{n-3} x \mp \cdots \right].](/pictures/eswiki/48/000aa963b1d0dc15b8533ffb85761921.png)
![\frac{\sin (nx)}{(\sin x)^n} = \left[ {n \choose 1} \cot^{n-1} x - {n \choose 3} \cot^{n-3} x \mp \cdots \right].](/pictures/eswiki/50/21f1c5e675d75afdc05090694209b8ee.png)