Un cuadrado latino es una matriz de n×n elementos, en la que cada casilla está ocupada por uno de los n símbolos de tal modo que cada uno de ellos aparece exactamente una vez en cada columna y en cada fila.

Las siguientes matrices son cuadrados latinos:

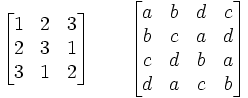
Los cuadrados latinos se dan como una Tabla de multiplicar (Tabla Cayley) de quasigrupos. Estos tienen su aplicación en el diseño de experimentos.

El nombre de Cuadrados Latinos se origina con Leonhard Euler quién utilizó caracteres Latinos como símbolos.

Un cuadrado latino se dice que está reducido (o normalizado o de forma estandarizada) si la primera fila y la primera columna están en orden natural. Por ejemplo, el primer cuadrado está reducido, porque la primera fila y la primera columna son 1, 2, 3.

Es posible hacer un cuadrado latino permutando (reordenando) las filas y las columnas.

Contenido 1 Representación por un Arreglo Ortogonal 2 Clases equivalente de Cuadrados latinos 3 El número de Cuadrados Latinos 4 Cuadrados Latinos y rompecabezas matemáticos 5 Véase también 6 Enlaces externos

Representación por un Arreglo Ortogonal

Si cada entrada de un cuadrado latino de n × n se escribe como una tripleta (f, c, s) donde f es la fila, c la columna y s el símbolo (para nuestro caso un número), obtenemos n² tripletas llamado arreglo ortogonal del cuadrado. Por ejemplo, para el primer cuadrado latino de nuestros ejemplos, el arreglo ortogonal será así

{ (1,1,1),(1,2,2),(1,3,3),(2,1,2),(2,2,3),(2,3,1),(3,1,3),(3,2,1),(3,3,2) },

donde, por ejemplo, la tripleta (2,3,1) representa que el valor en la fila 2 columna 3 es 1. La representación de un cuadrado latino puede ser escrita en términos del arreglo ortogonal quedando así:

• Existen n² tripletas de la forma (f, c, s), donde 1 ≤ f, c, s ≤ n.
• Todos los pares (f, c) son diferentes, todos los pares (f, s) son diferentes, y todos los pares (c, s) son diferentes.

La representación por arreglos ortogonales muestra que las filas, columnas y símbolos juegan un papel muy similar, esto estará un poco más claro conforme nos adentremos en el tema.

Clases equivalente de Cuadrados latinos

Muchas operaciones sobre un Cuadrado latino produce otro Cuadrado latino (por ejemplo, alternar filas).

Si permutamos las filas, permutamos las columnas, y permutamos los símbolos de un Cuadrado latino obtenemos un nuevo Cuadrado latino que decimos que es isotópico del primero. El isotopismo es una relación de equivalencia, en base a esto se dice que todos los Cuadrados latinos están divididos en subgrupos, llamados clases isotópicas, según esto dos Cuadrados de la misma clase se dice que son isotópicos, y dos de clases diferentes son no isotópicos.

Otro tipo de operación es simple de explicar usando la representación de estos por arreglos ortogonales. Si reorganizamos consciente y sistemáticamente los tres elementos de cada tripleta (f, c, s) por (c, f, s) lo cual corresponde a una transposición del cuadrado (reflejado en la diagonal principal), o podemos remplazar cada tripleta (f, c, s) por (c, s, f), lo que es una operación más complicada. Todas juntas nos dan 6 posibilidades, incluida no hacer nada, dándonos 6 Cuadrados Latinos llamados conjugados del cuadrado original.

Finalmente, podemos combinar estas dos operaciones equivalentes: Dos Cuadrados Latinos son paratópicos si uno de ellos es conjugado del otro. Esto es nuevamente una relación de equivalencia, con la clase de equivalencia principal llamada Clase Principal, especies o clase paratópica. Cada clase contiene 6 clases isotópicas.

El número de Cuadrados Latinos

No se conoce una fórmula para el cálculo fácil del número de Cuadrados Latinos de n × n son para n=1,2,...,n. Los límites superiores e inferiores más exactos conocidos para n más grande están demasiado separados. Aquí disponemos de todos los valores exactos conocidos. Es posible notar que los números crecen exageradamente rápido.

Para cada n, el número de Cuadrados Latinos disponibles (secuencia A002860 en OEIS ) es n! (n-1)! veces el número de Cuadrados Latinos reducidos (secuencia A000315 en OEIS).

El número de Cuadrados Latinos de distintos tamaños

n	Cuadrados Latinos reducidos de tamaño n	Todos los Cuadrados Latinos de tamaño n
1	1	1
2	1	2
3	1	12
4	4	576
5	56	161280
6	9408	812851200
7	16942080	61479419904000
8	535281401856	108776032459082956800
9	377597570964258816	5524751496156892842531225600
10	7580721483160132811489280	9982437658213039871725064756920320000
11	5363937773277371298119673540771840	776966836171770144107444346734230682311065600000

Para cada n, cada clase isotópica (secuencia A040082 en OEIS ) contiene arriba de (n!)³ Cuadrados Latinos (el número exacto varia), y cada clase principal (secuencia A003090 en OEIS ) contiene alguna de las 1, 2, 3 o 6 clases isotópicas.

Clases Equivalentes de Cuadrados Latinos

n	clases principales	clases isotópicas
1	1	1
2	1	1
3	1	1
4	2	2
5	2	2
6	12	22
7	147	564
8	283657	1676267
9	19270853541	115618721533
10	34817397894749939	208904371354363006

Cuadrados Latinos y rompecabezas matemáticos

El popular rompecabezas Sudoku es un caso especial de Cuadrados Latinos; toda solución de un Sudoku es un Cuadrado Latino. Un Sudoku impone una restricción adicional a los subgrupos de 3×3, estos solo deben contener los dígitos del 1 al 9 (en la versión estándar).

El rompecabezas conocido como Diamante 16 (Diamond 16 Puzzle) ilustra un concepto generalizado de la ortogonalidad de los Cuadrados Latinos: El Cuadrado Ortogonal ([1], 1976) o "Matrices ortogonales"-- ortogonal en el sentido combinatorio y no en un sentido algebraico-lineal (A. E. Brouwer, 1991).

Para una comparación con la Geometría Finita, ver Geometría del Cuadrado Latino (Inglés).

Véase también

• Cuadrado mágico
• Sudoku

Enlaces externos

• Latin Squares in Java at cut-the-knot (inglés)
• Infinite Latin Square (Java) at cut-the-knot (inglés)
• Magic Square in Latin Square (inglés)