Cuadro de oposición de los juicios

Cuadro de oposición de los juicios

Cuadro de oposición de los juicios

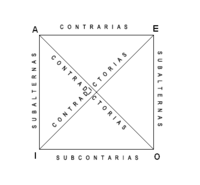
Se llama cuadro de oposición de los juicios al esquema mediante el que se estudian las relaciones formales entre los diversos tipos de juicios aristotélicos, A, E, I, O, considerando cada juicio con términos idénticos. En su día fue con considerado por el mismo Aristóteles.


A= UNIVERSAL AFIRMATIVO. Sujeto tomado en su extensión universal; predicado particular; relación afirmativa. Todo S es P.

E = UNIVERSAL NEGATIVO. Sujeto tomado en su extensión universal; predicado universal; relación negativa. Ningún S es P.

I = PARTICULAR AFIRMATIVO. Sujeto tomado en su extensión particular; predicado en su extensión particular; relación afirmativa. Algún S es P.

O = PARTICULAR NEGATIVO. Sujeto tomado en su extensión particular; predicado en su extensión universal; relación negativa. Algún S no es P.

Cuadro de oposición


Se llaman juicios opuestos a los que teniendo los mismos términos difieren en cantidad, en cualidad o en ambas. Se representan en cada uno de los vértices del cuadrado de oposición, estableciéndose las siguientes relaciones:

A y E son contrarios porque difieren en cualidad siendo universales.

I y O son subcontrarios, porque siendo particulares difieren en la cualidad.

A con respecto a O, e I con respecto a E son contradictorios, porque difieren en cantidad y cualidad.

A con respecto a I, y E con respecto a O son subalternos porque difieren en la cantidad.

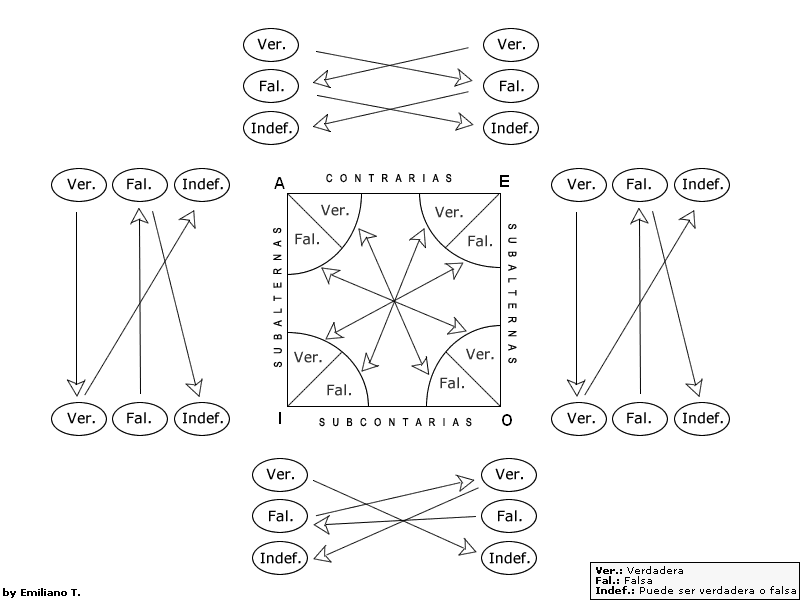
Las relaciones con respecto al valor de verdad en relación de unos y otros se muestran en el siguiente cuadro:

Los contradictorios, si uno es verdadero el otro es falso y viceversa. Ni ambos verdaderos, ni ambos falsos.

Los contrarios, no pueden ser ambos verdaderos, pero pueden ser los dos falsos.

Los subcontarios pueden ser ambos verdaderos, pero no pueden ser los dos falsos.

Para otras posibles inferencias directas a partir de un juicio es necesario hacer unas operaciones que producen nuevos juicios: la conversión y la obversión, contraposición e inversión.

Cuadro de oposición - Valores de Verdad
A E I O
A es verdadero V F V F
A es falso F Ind. Ind. V
E es verdadero F V F V
E es falso Ind. F V Ind.
I es verdadero Ind. F V Ind.
I es Falso Ind. V F V
O es Verdadero F V Ind. V
O es Falso V F V F

V= Verdadera F=Falsa Ind.= Indeterminada


Enlaces

Referencias

  • MITCHELL, D (1968). Introducción a la lógica. Editorial Labor, Barcelona.
  • FERRATER MORA, J. (1979). DICCIONARIO DE FILOSOFÍA.
Obtenido de "Cuadro de oposici%C3%B3n de los juicios"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Silogismo — El silogismo es una forma de razonamiento deductivo que consta de dos proposiciones como premisas y otra como conclusión, siendo la última una inferencia necesariamente deductiva de las otras dos. Fue formulado por primera vez por Aristóteles, en …   Wikipedia Español

  • Inferencia — Una inferencia es una evaluación que realiza la mente entre expresiones bien formadas de un lenguaje (EBF) que, al ser relacionadas intelectualmente como abstracción, permiten trazar una línea lógica de condición o implicación lógica entre las… …   Wikipedia Español

  • Silogismo categórico — El cuadro de oposición de los juicios muestra las relaciones entre los cuatro tipos de proposiciones categóricas. Un silogismo categórico es un silogismo compuesto por exactamente tres proposiciones categóricas (dos premisas y una conclusión) …   Wikipedia Español

  • Lógica de primer orden — La lógica de primer orden, también llamada lógica de predicados o cálculo de predicados, es un sistema formal diseñado para estudiar la inferencia en los lenguajes de primer orden.[1] Los lenguajes de primer orden son, a su vez, lenguajes… …   Wikipedia Español

  • Lógica — La lógica es una ciencia formal y una rama de la filosofía que estudia los principios de la demostración e inferencia válida. La palabra deriva del griego antiguo λογική (logike), que significa «dotado de razón, intelectual, dialéctico,… …   Wikipedia Español

  • Teoría formal — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Contraposición lógica — es una de las operaciones que la lógica clásica tradicional admitía como operación lógica. Consiste en la modificación del juicio aristotélico convirtiendo el juicio previamente obvertido, u obvirtiendo el juicio previamente convertido. De esta… …   Wikipedia Español

  • Ernesto Guevara — Ernesto Che Guevara Ernesto Guevara (imagen tomada por Alberto Korda el 5 de marzo de 1960) …   Wikipedia Español

  • Cristina Fernández de Kirchner — Saltar a navegación, búsqueda Cristina Fernández de Kirchner …   Wikipedia Español

  • Terrorismo de Estado en Argentina en las décadas de 1970 y 1980 — Este artículo o sección puede ser demasiado extenso(a). Algunos navegadores pueden tener dificultades al mostrar este artículo. Por favor, considera separar cada sección por a …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”