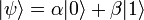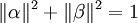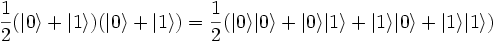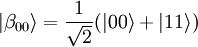Un qubit (del inglés qubit, de quantum bit, bit cuántico) es la unidad mínima y por lo tanto constitutiva de la información cuántica. Esta información puede representarse mediante el estado de un sistema cuántico binario (como por ejemplo, el spin de un electrón). Matemáticamente, puede describirse como un vector de módulo unidad en un espacio vectorial complejo bidimensional. Los dos estados básicos de un qubit son |0> y |1>, que corresponden al 0 y 1 del bit clásico (se pronuncian: ket cero y ket uno). Pero además, el qubit puede encontrarse en un estado de superposición cuántica (también denominado estado qubital puro) combinación de esos dos estados (α | 0 > + β | 1 > ). En esto es significativamente distinto al estado de un bit clásico, que puede tomar solamente los valores 0 o 1.

Contenido 1 Origen 2 Estados del qubit 3 Paralelismo cuántico 4 Entrelazamiento cuántico 5 Representación física 6 Registro cuántico 7 Unidades derivadas 8 Véase también 9 Enlaces externos

Origen

Benjamin Schumacher descubrió la forma de interpretar los estados cuánticos como información y acuñó el término qubit. También descubrió una manera de comprimir la información en un estado y de almacenar la información en el número más pequeño de estados. Es la analogía cuántica de la teoría de la información clásica de Shannon y ahora se conoce como compresión de Schumacher.

Estados del qubit

Un qubit, en general, se presenta como una superposición o combinación lineal de los estados básicos 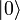y 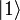. Esta superposición se denomina estado qubital puro y puede representarse como:

donde las amplitudes de probabilidad α y β son en general números complejos. A partir de estos coeficientes se determina la probabilidad de obtener en una medida los resultados 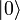y 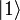. En concreto, si realizamos una medida de la información contenida en el qubit podemos obtener el resultado 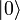con probabilidad |α|² o el resultado 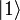con probabilidad |β|². Puesto que la probabilidad total tiene que ser la unidad, α y β se deben relacionar por la ecuación:

Esta ecuación simplemente asegura que en la medición se obtiene un estado o el otro. Debido a su naturaleza mecánica cuántica, cualquier medida del qubit altera inevitablemente su estado. Un qubit puede existir en un estado de superposición de los estados de base, pero la medida del qubit ocasiona que la superposición colapse a uno de los estados base, según las probabilidades mencionadas arriba.

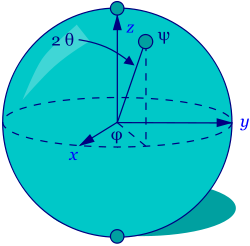
El espacio de estados del qubit se puede representar mediante un espacio vectorial complejo bidimensional de módulo 1. Equivalentemente, se puede representar de forma geométrica por la esfera de Bloch. Cada estado del qubit corresponde a un punto de la superficie de una esfera de radio unidad. Esto esencialmente significa que un qubit tiene dos grados de libertad locales. Estos grados de libertad podrían ser la longitud y latitud, o como es más habitual, dos ángulos.

Paralelismo cuántico

Ya se ha indicado una de las diferencias entre bit y qubit: un bit toma valores discretos mientras que los valores representados por un qubit son de naturaleza continua. Sin embargo, esta característica podría replicarse con magnitudes continuas clásicas (longitudes, voltajes, etc).

Una segunda diferencia es el paralelismo cuántico, que es la posibilidad de representar simultáneamente los valores 0 y 1. Los algoritmos cuánticos que operan sobre estados de superposición realizan simultáneamente las operaciones sobre todas las combinaciones de las entradas. Por ejemplo, los dos qubits

representan simultáneamente las combinaciones 00, 01, 10 y 11. En este "paralelismo cuántico" se cifra la potencia del cómputo cuántico.

Entrelazamiento cuántico

Una tercera característica importante que distingue al qubit del bit clásico es que múltiples qubits pueden presentarse en un estado de entrelazamiento cuántico. En el estado no entrelazado 1 / 2( | 0 > | 0 > + | 0 > | 1 > + | 1 > | 0 > + | 1 > | 1 > ) pueden darse las cuatro posibilidades: que la medida del primer qubit dé 0 o 1 y que la medida del segundo qubit dé 0 o 1. Esto es posible porque los dos qubits de la combinación son separables (factorizables), pues la expresión anterior puede escribirse como el producto de ( | 0 > + | 1 > ) y ( | 0 > + | 1 > ).

El entrelazamiento es una característica no local que permite que un sistema de qubits se exprese con una correlación más alta que la posible en sistemas clásicos. Un sistema de dos qubits entrelazados no puede descomponerse en factores independientes para cada uno de los qubits. Sea, por ejemplo, el entrelazamiento de dos qubits en un estado de Bell:

(Nota: en este estado las probabilidades de obtener |00> o |11> son iguales.)

Supongamos que uno de estos dos qubits entrelazados se entrega a Alicia y el otro a Bob. Alicia hace la medida de su qubit, y supongamos que obtiene el valor 0. Debido al entrelazamiento de los qubits, si Bob hace ahora su medida, conseguirá el mismo valor que Alicia, es decir, debe obtener 0. Esto es porque no existe el término |01>. De la misma forma, si Alicia hace su medida y obtiene el valor 1, y Bob la hace después, deberá obtener obligatoriamente 1 (puesto que no existe el término |10>). De esta forma, el resultado que obtiene Bob está condicionado por el que obtenga Alicia, aunque estén separados por años luz de distancia.

Este estado puede utilizarse para realizar la teleportación cuántica.

Representación física

Cualquier sistema cuántico de dos niveles se puede utilizar para representar un qubit. Los sistemas de niveles múltiples se pueden utilizar también, si poseen dos estados que se puedan desemparejar con eficacia del resto (por ejemplo, el estado fundamental y el primer estado excitado de un oscilador no lineal). Hay varias opciones de este tipo de sistemas que se han puesto en práctica con éxito. Además, distintas implementaciones de qubits podrían emplearse juntas para construir un computador cuántico, de la misma forma que se hace en la computación clásica, en donde un bit puede representarse mediante el estado de un transistor en una memoria, por el estado de magnetización de un disco duro o por la transmisión de corriente en un cable.

Registro cuántico

Varios qubits juntos forman un registro de qubits o registro cuántico. Las computadoras u ordenadores cuánticos ejecutan algoritmos cuánticos manipulando qubits, tales como el algoritmo de Shor que descompone en factores un número N con una complejidad computacional en tiempo O((logN)³) y en espacio O(logN).

Unidades derivadas

• Qutrit: Es una unidad cuántica de 3 estados. Éstos se representan convencionalmente por: |0>, |1> y |2> (Ket cero, ket uno y ket dos).

Véase también

• Computación cuántica
• Quantum
• Qutrit

Enlaces externos

• La organización cofundada por uno de los pioneros en computación cuántica, David Deutsch (en inglés)
• Del bit al qubit
• Monografía: Computadores Cuánticos, por Jesús Peña 2007.
• Definición de Qubit
• Definición de Qubit (En inglés)
• ¿Qué es un Qubit? 2003.