- Cuerno de Gabriel
-
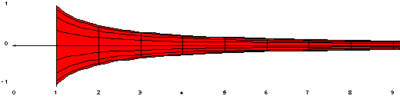
El Cuerno de Gabriel (también llamado Trompeta de Torricelli) es una figura geométrica ideada por Evangelista Torricelli que tiene la característica de poseer una superficie infinita pero un volumen finito.
Imagen parcial del Cuerno de Gabriel (o Trompeta de Torricelli).
Contenido
Historia
En el momento de su descubrimiento, fue considerado una paradoja. Esta paradoja aparente ha sido descrita de modo informal señalando que sería necesaria una cantidad infinita de pintura para cubrir la superficie interior, mientras que sería posible rellenar toda la figura con una cantidad finita de pintura y así cubrir esa superficie.
La solución de la paradoja es que un área infinita requiere una cantidad infinita de pintura si la capa de pintura tiene un grosor constante. Esto no se cumple en el interior del cuerno, ya que la mayor parte de la longitud de la figura no es accesible a la pintura, especialmente cuando su diámetro es menor que el de una molécula de pintura. Si se considera una pintura sin grosor, sería necesaria una cantidad infinita de tiempo para que ésta llegase hasta el «final» del cuerno.
En otras palabras, llegaría un momento en el que el espesor de la trompeta sería más pequeño que una molécula de pintura con lo que, digamos, una gota de pintura cubriría el resto de la superficie de la trompeta (aunque fuera infinito). Así, que la superficie de la trompeta sea infinita no implicaría que la cantidad de pintura tenga que ser infinita.
Pero la paradoja también tiene solución incluso si suponemos una materia divisible indefinidamente (o sea, si no existen los átomos). Si el grosor de la capa de pintura es variable y disminuye indefinidamente (tendiendo a cero), la cantidad de pintura se calcularía por una integral impropia que podría ser convergente. En este caso, el espesor de la capa de pintura forzosamente debería ser igual o menor al valor de y, lo que hace que la integral impropia, en este caso, sea convergente, es decir, se necesita una cantidad finita de pintura.
Ecuación matemática
El cuerno de Gabriel se forma utilizando la gráfica de
, con el rango 
(para evitar la asíntota en x = 0), y rotándola en tres dimensiones alrededor del eje X. Su descubrimiento es anterior al cálculo, pero es fácil de verificar integrando que su área superficial y su volumen están dados, respectivamente por, 
y 
.Si se considera la parte del cuerno entre x = 1 y x = a, el área de la superficie es más que 2πln(a) y el volumen es
.Cuando a aumenta, el área no está acotada, mientras que el volumen tiene una cota superior de π.
Véase también
Enlaces externos
- Weisstein, Eric W. Gabriel's Horn from MathWorld. (en inglés)
- Información y diagramas sobre el cuerno de Gabriel (en inglés)
Categorías:- Superficies
- Paradojas matemáticas
Wikimedia foundation. 2010.
