Superficie (matemática)

Ilustración de una superficie curvada, inmersa en , orientable y con borde; sobre la que se ha dibujado un conjunto de líneas coordenadas ortogonales.

Una superficie es de hecho un conjunto de puntos de un espacio euclídeo que forma un espacio topológico bidimensional que localmente, es decir, visto de cerca se parece al espacio euclídeo bidimensional. Así alrededor de cada punto de una superficie esta se aproxima bien por el plano tangente a la superficie en dicho punto.

Una definición tradicional de superficie que alude a términos intuitivos pero con la que resulta fácil trabajar desde un punto de vista matemático fue la dada por Euclides:

Definiciones formales

Una superficie es una variedad bidimensional, es decir, un objeto topológico que localmente "se parece" al plano euclídeo (técnicamente localmente homeomorfo al plano). Eso significa que si tomamos una porción muy pequeña de la superficie es parecida a al plano euclídeo, al igual que en medio de una llanura la superficie local de la tierra nos parece plana.

Más formalmente el homeomorfismo local entre una superficie y el plano euclídeo implica que para cada punto de una superficie hay una vecindad de P (una pequeña región que la rodea) que es homeomorfa a un disco abierto de . Esta propiedad de ser homeomorfa con el plano permite construir un sistema de coordenadas local bidimensional en torno a cualquier punto en la superficie. Se puede llamar al homeomorfismo local que va de la superficie a como carta y al inverso (de este homeomorfismo) parametrización. No siempre es posible parametrizar una superficie con un único homeomorfismo local.

Una superficie (topológica) con frontera es un espacio topológico de tipo Hausdorff en que cada punto tiene una vecindad abierta V para la que existe un homeomorfismo φ con un conjunto abierto del semiplano superior del plano euclídeo . El par ordenado (V, φ) se llama carta (local) de coordenadas del punto [esta carta no es única porque para cada punto existen de hecho muchas posibles elecciones de coordenadas].

Propiedades y tipos de superficies

Las superficies usuales son versiones curvadas del plano, de hecho son localmente homeomorfas a él. No es extraño por tanto que varios tipos de superficies interesantes en las aplicaciones, se definan a partir de propiedades de curvatura respecto al plano euclídeo o en términos de isometrías. Además otros conceptos topológicos interesantes como la orientabilidad permiten expresar formalmente ciertas propiedades de las superficies.

Superficies cerradas

Un ejemplo de una superficie cerrada y múltiplemente conexa es el triple toro.

Intuitivamente una superfice cerrada en el espacio tridimensional es cualquier superfice que encierra un volumen, dividiendo a dicho espacio en una región "acotada" y una región "no acotada". En 4 o más dimensiones también existen superficies cerradas pero la noción intuitiva anterior no es válida, ya que las superficies cerradas en más dimensiones no dividen al espacio de esta forma. Por esa razón para definir que es una superificie cerrada se recurre a definición más formal que usa el concepto de "frontera topológica":

Una superficie cerrada es una superficie que no tiene frontera.

• Puede comprobarse que en tres dimensiones una superficie sin frontera encierra un volumen, como por ejemplo la esfera y el toro o "donut", estas superficies son además superficies orientables. De hecho todas las superficies cerradas inmersas en el espacio tridimensional son orientables, a diferencia de lo que ocurre en más dimensiones.
• Otras superficies cerradas más exóticas son el plano proyectivo y la botella de Klein (definible en 4 dimensiones).
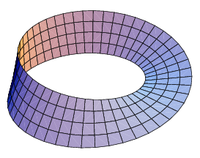
• Un disco (en ), un cilindro y la banda de Möbius son ejemplos de superficies con frontera. Como la imagen de la derecha.

Superficies desarrollables, regladas y alabeadas

Algunas superficies tienen propiedades interesantes que son expresables en términos de su curvatura, estos tipos son las superficies desarrollables, regladas y alabeadas:

• Intuitivamente una superficie es desarrollable si puede fabricarse a partir de un plano euclídeo mediante "doblado". El cono y el cilindro son desarrollables, lo cual se manifiesta en que se pueden construir modelos apropiados a partir de una hoja de papel o cartulina plana. Formalmente dada una superficie desarrollable existe una isometría entre la superficie y el plano euclídeo. Una condición necesaria y suficiente para que una superficie se desarrollable, se desprende del theorema egregium de Gauss, es que la curvatura gaussiana de dicha superficie sea idénticamente nula.
• Una superfice reglada cuando el plano tangente para cada punto de la misma contiene una línea recta completamente contenida sobre la superficie. Una condición necesaria es que la segunda forma fundamental sea en ese punto una forma cuadrática indefinida y por tanto la curvatura gaussiana es negativa.
• Una superficie alabeada es una superficie reglada y no-desarrollable.

Superficies orientables

La banda de Möbius es una superficie no-orientable con una frontera (su frontera es una curva cerrada simple).

Una última propiedad menos intutiva es la de orientabilidad, que permite distinguir entre superficies orientables y no-orientables. Una superficie orientable puede definirse simplemente como una variedad orientable de dimensión dos, donde toda curva cerrada simple contenida, tiene una vecindad regular homeomorfa a un cilindro abierto. Cualquier variedad de dimensión dos que no es orientable es una superficie no-orientable. Esto es, existe al menos una curva cerrada simple contenida, que tiene una vecindad regular homeomorfa a una banda de Möbius.

Las superficies orientables cerradas tienen la propiedad de dividir el espacio tridimensional (donde siempre pueden ser encajadas) en dos regiones diferentes y disjuntas: una acotada por dicha superficie que es de volumen finito y otra no acotada exterior a dicho volumen.

Este término se utiliza para distinguirlas de las superficies que no encierran nada en su interior, como un plano infinito en referencia al espacio tridimensional. Es imposible hablar de que las superficies no orientables dividan el espacio tridimensional pues estas superficies no pueden ser encajadas en él.

Teorema de clasificación de superficies cerradas

Un importante resultado matemático es el teorema de clasificación de superficies cerradas, el cual afirma que toda superficie cerrada (es decir, compacta y sin frontera o borde) es homeomorfa a algún miembro de las siguientes tres familias de superficies:

1. la esfera;
2. la suma conexa de -toros, siendo ;
3. la suma conexa de k planos proyectivos reales, siendo .

Dicho de otra manera, las superficies anteriores son todas las superficies cerradas que existen (salvo homeomorfismo). La superficies de las dos primeras familias son orientables. Es conveniente combinar las dos primeras familias, considerando la esfera como la suma conexa de cero toros. El número g de toros involucrados en la construcción se denomina género de la superficie. Puesto que la esfera y el toro tienen características de Euler 2 y 0, respectivamente, se deduce que la característica de Euler de la suma conexa de g toros es precisamente .

Deformando una 2-variedad con frontera.

Las superficies de la tercera familia son no-orientables. La característica de Euler del plano proyectivo real es 1, así la suma conexa de k de ellos es is .

De todo esto se sigue, que una superficie cerrada está determinada -salvo homeomorfismo- por dos propiedades: el valor numérico de su característica de Euler (o su género) y si es o no-orientable.

Es posible clasificar también las superficies que no son cerradas (es decir, con frontera). Esto se obtiene como el esquema anterior, añadiendo el número de fronteras que tiene la superficie.

Véase también

• Variedad diferenciable
• Variedad algebraica
• Variedad topológica
• Geometría diferencial de superficies
• Área

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Superficie (matemática). Commons
• Surface en la Enciclopedia en-línea de la Springer-Verlag
• Clasificación de las superficies, en webdelprofesor.ula.ve