En probabilidad y estadística, la cuota a favor de un evento o proposición se calcula mediante la fórmula 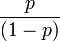, dónde p es la probabilidad del evento o proposición. La cuota en contra del mismo evento se calcula mediante la fórmula 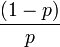. Por ejemplo, al escoger al azar un día de la semana (7 días), la cuota asociada a favor de un domingo cualquiera es 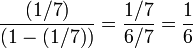, no , como podría parecer. La cuota en contra del mismo domingo es 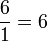; eso significa que es 6 veces más probable que no sea domingo a que sí sea domingo. Estas cuotas son relativas a la probabilidad de suceder.

Generalmente las cuotas no son determinadas por el público en general a causa de la confusión natural que se tiene con la probabilidad de un suceso expresada de forma fraccionaria. De esta forma, la probabilidad al escoger al azar un domingo respeto a todos los días de la semana es de uno a siete (1/7). Un corredor de apuestas (para sus propios propósitos) utilizará las cuotas en formato uno contra seis, expresada generalmente por la mayoría de personas como 6 a 1, 6-1, o 6/1 (leído como seis a uno) donde la primera cifra representa el número de días contrarios al éxito del suceso, y la segunda cifra corresponde al los días a favor del éxito del suceso (cuotas a favor). En otras palabras, un evento con m a n de cuotas en contra, tendrá una probabilidad de n/(m + n), mientras que un evento de m a n de cuotas a favor, la probabilidad será de m/(m + n). La teoría de la probabilidad expresa que las cuotas juegan un papel más natural o más conveniente que las probabilidades.

Para algunos juegos de azar, puede ser también la forma más conveniente para que el apostante entienda mejor cuantas ganancias tendrá si su selección es la correcta: al individuo le pagaran seis por cada unidad apostada. Por ejemplo, una apuesta ganadora de 10 € se pagará a 6 x 10€ = 60€, retornando también los 10 € originales de la apuesta.

Presentación de las cuotas

Escogiendo un evento cualquiera con una probabilidad de 1 a 5 de éxito (1/5, 0.2 o 20%), la cuota es de 0.2/(1- 0.2) = 0.2 / 0.8 = 0.25. Este valor (0.25) representa la cantidad a apostar necesaria para que la ganancia de la apuesta a favor en caso de que ocurra el acontecimiento sea de una unidad. Este valor se puede escalar por un factor de conveniencia para dar a la cifra el valor más conveniente. Por ejemplo, si una apuesta de 0.25 unidades tiene una ganancia de 1, podemos escalar x4 los valores, de forma que en una apuesta de 1 unidad la ganancia será de 4. Si se apuesta 1 unidad a favor del acontecimiento de este evento, la ganancia será de 4 unidades más la unidad original apostada. Este hecho puede estar representado por cuotas fraccionarias 4/1, por cuotas decimales 5.0 (incluyendo el importe de la apuesta original) o por cuotas americanas +400 (representando la ganancia sobre una apuesta de 100).

Por contraste, un evento cualquiera con una probabilidad de 4 a 5 de éxito (4/5, 0.8 o 80%), la cuota es de 0.8/(1- 0.8) = 0.8 / 0.2 = 4. En una apuesta a favor de este evento, se recibirá una unidad más de la apuesta original (4 unidades). Estará representado por cuotas fraccionarias como a 1/4, en cuotas decimales como a 1.25 y en cuotas americanas como a -400, representando la apuesta necesaria para una ganancia de 100.

Cuotas en las apuestas vs. cuotas en las probabilidades

En el juego, las cuotas de las apuestas no representan la probabilidad real de éxito del evento. Representa la cantidad que las casas de apuestas pagaran por las apuestas ganadoras. Al calcular sus cuotas las casas de apuestas incluyen un margen de beneficio, el cual significará que lo que se pagará por una apuesta ganadora será menos que la probabilidad real de que el suceso ocurra.^[1] Este margen es conocido como redondeo de las cuotas. Veamos aquí un ejemplo:

En una carrera de 3 caballos, la probabilidad real de que cada caballo gane la carrera es de 50%, 40% y 10%. Estas son las probabilidades relativas de que cada caballo gane la carrera. El total de los porcentajes es de 100, representando así una probabilidad justa. Las cuotas correspondientes para cada un de los tres caballos serían de 2-1, 6-4 y 9-1 respectivamente (2, 2.5 y 10 respectivamente en cuotas decimales).

Para conseguir beneficios en las apuestas aceptadas, las casas de apuestas incrementan los valores de estas probabilidades a 60%, 50% y 20% para los tres caballos, representando unas cuotas de 4-6, 2-1 y 4-1 respectivamente (1.67, 2 y 5 respectivamente en cuotas decimales). Estos valores ahora suman un total de 130. Esto significa que para la casa de apuestas el redondeo de las cuotas le supone un beneficio de 30 (130 – 100) si las apuestas aceptadas se corresponden en sus proporciones correctas para cada caballo. El arte en el correteo de las apuestas se trata justamente de esto, de recibir unos 130€ para esta apuesta y retornar unos 100€, incluyendo las apuestas iniciales, independientemente del caballo ganador.

La ganancia en las apuestas tiene en cuenta la relación entre las probabilidades reales de éxito de un acontecimiento y la cuota ofrecida. Si uno puede conseguir que las cuotas de las apuestas hechas se paguen por encima de las cuotas reales del evento, en teoría se conseguirán ganancias. Este tipo de apuestas se llaman valuebets (apuestas valiosas).^[1] Los servicios informativos de deportes son utilizados a menudo por apostantes profesionales o semiprofesionales en la búsqueda de estas apuestas.

Las cuotas o las cantidades que las casas o los corredores de apuestas pagan vienen determinadas también por la cantidad apostada en cada posible caso del evento. Se trata de balancear las cuotas de forma que las apuestas se repartan de forma proporcionada para cada una de las posibilidades.

Referencias

1. ↑ ^{a b} Arbedia: Explicación sobre los Valuebets

Enlaces externos

• Arbedia, Gestor de surebets y valuebets