Función definida a trozos

Función definida a trozos

En matemáticas, una función definida a trozos (también conocida como función por partes) es una función cuya definición (la regla que define la dependencia) cambia dependiendo del valor de la variable independiente. Matemáticamente, una función real f (definida a trozos) de una variable real x es la relación cuya definición está dada por varios conjuntos disjuntos de su dominio (conocidos como subdominios).

La palabra "A trozos" se usa para describir cualquier propiedad de una función definida a trozos que se cumple para cada trozo aunque podría no cumplirse para todo el dominio de f. Una función es diferenciable a trozos o continuamente diferenciable a trozos si cada trozo es diferenciable a lo largo del dominio. En Análisis Convexo, la noción de la derivada puede ser reemplazada por la de subderivada para funciones definidas a trozos. Una función f definida a trozos puede estar representada por varias expresiones matemáticas (algebraicas y/o trascendentales) de cualquier tipo.

Contenido

Notación e interpretación

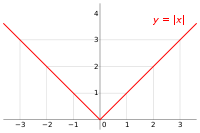
Gráfica de la función valor absoluto, y = |x|.

Las funciones definidas a trozos se expresan con una notación funcional común, donde el cuerpo de la función es una lista de expresiones matemáticas asociadas a un subdominio (intervalo). Por ejemplo, sea la función f definida a trozos de la función valor absoluto:

|x| \equiv f(x) = \begin{cases} -x, & \mbox{si } x < 0 \\ x, & \mbox{si } x \ge 0 \end{cases}

Para todos los valores de x menores que cero, la primera expresión matemática (la función -x) es utilizada, lo que altera el signo del valor que asignamos a la variable independiente haciendo el resultado siempre positivo. Para todos los valores de x mayores o iguales que cero, la segunda expresión matemática (la función x) es utilizada.

Sea la función definida a trozos f(x), se evalúan varias expresiones del dominio de f:

x f(x) Función utilizada
−3 3 −x
−0.1 0.1 −x
0 0 x
1/2 1/2 x
5 5 x

Por lo tanto, para evaluar una función definida a trozos en un determinado valor del dominio, seleccionamos la expresión matemática cuyo subdominio contiene el valor a evaluar para que el valor del rango sea el correcto.

Continuidad

Una función definida a trozos con diferentes funciones cuadráticas a cada lado de x0.

Una función definida a trozos es continua en un intervalo dado si está definida en todo el intervalo, las expresiones matemáticas apropiadas que constituyen a la función son continuas en ese intervalo, y no hay discontinuidad en ningún punto extremo de los subdominios en ese intervalo.

La función que está a la derecha, por ejemplo, es una función definida a trozos continua en todos sus subdominios, pero no es continua en todo el dominio. Dicha función tiene un salto de discontinuidad (un agujero) en x0.

Véase también

Ejemplos comunes


Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Función continua — En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente… …   Wikipedia Español

  • Función escalonada — Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c1 < c2 < ... < cn, y en cada intervalo ]ck, ck+1[ es constante,… …   Wikipedia Español

  • Función indicatriz — Gráfico de una función indicatríz que muestra a un subconjunto de los puntos de un cuadrado (en rojo), donde los puntos tienen coordenada z=1 (color ocre), mientras que los puntos del cuadrado …   Wikipedia Español

  • Función signo — En matemática, la función signo es una función matemática especial, una función definida a trozos, que obtiene el signo de cualquier número real que se tome por entrada. Se representa generalmente mediante sgn(x), y no debe confundirse con la… …   Wikipedia Español

  • Spline — Un tipo de spline, una curva de Bézier. En el subcampo matemático del análisis numérico, un spline es una curva diferenciable definida en porciones mediante polinomios. En los problemas de interpolación, se utiliza a menudo la interpolación… …   Wikipedia Español

  • Parámetro estadístico — Saltar a navegación, búsqueda La media aritmética …   Wikipedia Español

  • Flitro de coseno alzado — Saltar a navegación, búsqueda Un filtro de coseno alzado es un tipo de filtro electrónico, utilizado frecuentemente en sistemas de telecomunicaciones debido a que es capaz de reducir al mínimo la interferencia entre símbolos (ISI). Se llama así… …   Wikipedia Español

  • Integración — La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos. Para otros usos de este término, véase Integración …   Wikipedia Español

  • Densidad espectral — Saltar a navegación, búsqueda DEP de una señal aleatoria en la banda de 0kHz 20kHz estimada mediante el método de Welch En matemáticas y en física, la Densidad Espectral (Spectral Density) de una señal es una función matemática que nos informa de …   Wikipedia Español

  • Indicador Myers-Briggs — El Indicador de Myers Briggs (o MBTI por sus siglas en inglés) es un test de personalidad diseñado para ayudar a una persona a identificar algunas de sus preferencias personales más importantes. El indicador fue creado por Katharine Cook Briggs y …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”