Función de densidad de probabilidad

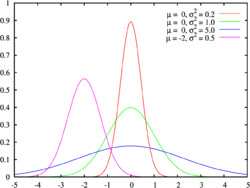Función de densidad de probabilidad para la distribución normal.

En teoría de la probabilidad, la función de densidad de probabilidad, función de densidad, o, simplemente, densidad de una variable aleatoria continua es una función, usualmente denominada f(x) que describe la densidad de la probabilidad en cada punto del espacio de tal manera que la probabilidad de que la variable aleatoria tome un valor dentro de un determinado conjunto sea la integral de la función de densidad sobre dicho conjunto.

Definición

Una función de densidad de probabilidad (FDP) es una función matemática que caracteriza el comportamiento probable de una población. Es una función f(x) que especifica la posibilidad relativa de que una variable aleatoria continua X tome un valor cercano a x, y se define como la probabilidad de que X tome un valor entre x y x+dx, dividido por dx, donde dx es un número infinitesimalmente pequeño. La mayoría de las funciones de densidad de probabilidad requieren uno o más parámetros para especificarlas totalmente.

La probabilidad de que una variable aleatoria continua X esté ubicada entre los valores a y b está dada por el intervalo de la FDP, f(x), comprendido en el rango entre a y b. ≤ < = ∫ a b Pr(a x b) f (x)dx La FDP es la derivada (cuando existe) de la función de distribución: f x dF x dx ( ) = ( ) En situaciones prácticas, la FDP utilizada se elige entre un número relativamente pequeño de FDP comunes, y la labor estadística principal consiste en estimar sus parámetros. Por lo tanto, a los efectos de los inventarios, es necesario saber qué FDP se ha utilizado e indicarlo en la documentación de evaluación de la incertidumbre.

La definición formal de la función de densidad requiere de conceptos de la teoría de la medida. Si una variable aleatoria X sigue una función de probabilidad X_*P su densidad con respecto a una medida de referencia μ es la derivada de Radon–Nikodym

$f = \frac{\mathrm d X_*\operatorname{P}}{\mathrm d \mu} .$

Es decir, ƒ es una función con la propiedad de que

$\mathrm P [X \in A ] = \int_{X^{-1}A} \, \mathrm d \operatorname{P} = \int_A f \, \mathrm d \mu$

para cada conjunto medible A.

Hay que advertir que la función de densidad no es propiamente única: dos funciones distintas pueden representar la misma distribución de probabilidad si son distintas únicamente en un conjunto de medida nula. Además, que puede haber distribuciones de probabilidad que carezcan de función de densidad: sucede cuando, sin ser discretas, concentran su probabilidad en conjuntos de medida nula; así sucede con la distribución de Cantor cuando se toma la de Lebesgue como medida de referencia.

Cuando, como ocurre normalmente en las aplicaciones, X es una variable aleatoria real y μ es la medida de Lebesgue, la función de densidad es una función tal que

$\operatorname P [a \leq X \leq b] = \int_a^b f(x) \, \mathrm{d}x .$

De modo que si F es la función de distribución de X, entonces

$F(x) = \int_{-\infty}^x f(u) \, \mathrm{d}u ,$

$f(x) = \frac{\mathrm{d}}{\mathrm{d}x} F(x) .$

Intuitivamente, se puede pensar que ƒ(x) dx es la probabilidad de que X asuma valores en el intervalo infinitesimal [x, x + dx].

Propiedades

De las propiedades de la función de distribución se siguen las siguientes propiedades de la fdp (a veces visto como pdf del inglés):

$f(x)\ge 0\;$ para toda $x$ .
El área total encerrada bajo la curva es igual a 1:

$\int_{-\infty}^\infty \,f(x)\,dx = 1$

La probabilidad de que $X$ tome un valor en el intervalo $[a, b]$ es el área bajo la curva de la función de densidad en ese intervalo o lo que es lo mismo, la integral definida en dicho intervalo. La gráfica f(x) se conoce a veces como curva de densidad.

$\Pr(a \leq X \leq b) = \int_{a}^{b} f(x)\,dx=F(b)-F(a)$

Algunas FDP están declaradas en rangos de $-\infty \;$ a $+\infty \;$ , como la de la distribución normal.

Enlaces externos

[1] Simulación de la obtención de la probabilidad en un intervalo a partir de la función de densidad de una variable continua con R (lenguaje de programación)

Véase también

Polinomio de Bernstein

Categoría:

Distribuciones de probabilidad

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Función de densidad — La función de densidad se utiliza en la ciencia estadística con el propósito de conocer cómo se distribuyen las probabilidades de un evento en relación al resultado del evento. En este caso se llama función de densidad de probabilidad.… … Enciclopedia Universal
Función cuantil — En probabilidad la función cuantil de una distribución de probabilidad es la inversa de la función de distribución.[1] Dada una función de distribución continua y estrictamente monótona, , la función cuantil, F −1, devuelve un valor x tal… … Wikipedia Español
Función de Cantor — En matemáticas, la función de Cantor, llamada así en honor de Georg Cantor, es un ejemplo de función matemática que es continua pero no absolutamente continua. También se la conoce como la escalera del Diablo. La función de Cantor guarda una… … Wikipedia Español
Densidad (mecánica cuántica) — Saltar a navegación, búsqueda En Mecánica cuántica las partículas no pueden ser consideradas puntuales, sino que se encuentran deslocalizadas espacialmente. La densidad (también llamada densidad de probabilidad) es una función que determina la… … Wikipedia Español
Función de ondas — Saltar a navegación, búsqueda Función de onda para una partícula bidimensional encerrada una caja, las líneas de nivel sobre el plano inferior están relacionadas con la probabilidad de presencia. En mecánica cuántica, una función de onda (Ψ) es… … Wikipedia Español
Función de onda — para una partícula bidimensional encerrada en una caja. Las líneas de nivel sobre el plano inferior están relacionadas con la probabilidad de presencia. En mecánica cuántica, una función de onda es una forma de representar el estado físico d … Wikipedia Español
Probabilidad uniforme — Saltar a navegación, búsqueda En estadística la distribución uniforme o probabilidad uniforme es una distribución de probabilidad continua con dos parámetros a y b cuya función de densidad es Integrando se obtiene la función de distribución: El… … Wikipedia Español
Densidad (desambiguación) — Saltar a navegación, búsqueda En demografía, densidad de población se refiere a la cantidad de seres por unidad de área. En lipoproteínas, densidad puede referirse a Lipoproteína de baja densidad (LDL) y a Lipoproteína de alta densidad. En… … Wikipedia Español
Función de verosimilitud — En estadística, la función de verosimilitud (o, simplemente, verosimilitud) es una función de los parámetros de un modelo estadístico que permite realizar inferencias acerca de su valor a partir de un conjunto de observaciones. No debe… … Wikipedia Español
Función de probabilidad — Para otros usos de este término, véase medida de probabilidad. En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia a cada punto de su espacio muestral X la… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Función de densidad de probabilidad

Contenido

Definición

Propiedades

Enlaces externos

Véase también

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Función de densidad de probabilidad

Contenido

Definición

Propiedades

Enlaces externos

Véase también

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo