Interacción espín-órbita

Interacción espín-órbita

Interacción espín-órbita

La interacción espín-órbita, en magnetoquímica, es la interacción magnética (cuántica) entre el momento magnético de espín y el momento magnético orbital. El acoplamiento espín-órbita es el acoplamiento entre estos momentos magnéticos.

Sólo lo encontramos cuando en un ion, además de electrones desparejados (que aportan momento magnético de espín) tenemos una configuración electrónica con degeneración orbital. En estos casos, coexisten la interacción electrostática (repulsión de Coulomb) con la magnética (interacción espín-órbita). Generalmente, se calcula usando la teoría perturbacional: se supone que una de las dos interacciones es mucho más intensa, y se trata a la menos intensa como una perturbación menor.

Esquema de Russell-Saunders

Este esquema supone que la interacción electrostática es mucho más intensa que la magnética. Esta condición es válida para los metales de la primera serie de transición, y progresivamente menos adecuada para la segunda y tercera. Se describe de forma análoga al canje magnético, con el siguiente hamiltoniano:

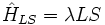
\hat{H}_{LS} = \lambda L S

donde L es el resultado del acoplamiento de los li individuales, S es el resultado del acoplamiento de los si individuales, y λ es positivo para capas de orbitales d menos que semillenas (d1-d4), negativo para capas más que semillenas (d6-d9) y nulo para capas vacías y semillenas. El acoplamiento de S y L es lo que da lugar al momento magnético global J.

La interacción espín-órbita así considerada está directamente relacionada con el desdoblamiento a campo nulo y con el factor g de Landé: si hay elongación axial en la coordinación del ion metálico, un λ positivo implica un g<2 y un D<0. Compresión axial y λ negativo tienen el mismo resultado, mientras que las otras dos combinaciones tienen el resultado opuesto (g>2 y D>0).

Esquema j-j

Este esquema es el opuesto al de Russell-Saunders, y se basa en una interacción magnética es mucho más intensa que la electrostática. Es válida especialmente para los actínidos, y, en menor medida, para los lantánidos. En este esquema se acoplan fuertemente las li y si para dar ji, y son éstas las que interaccionan para dar una J total.

Acoplamientos intermedios

Cuando es necesaria una aplicación simultánea de las dos interacciones, por ser de magnitud comparable, la resolución del problema presenta una complejidad mucho mayor, y no es posible llegar a soluciones analíticas generales. En estos casos, es útil e ilustrativo representar diagramas de correlación entre las dos aproximaciones anteriores. En general, éstos no presentarán una correspondencia biunívoca entre estados, sino que mostrarán mezclas, por la regla de no cruzamiento.

Obtenido de "Interacci%C3%B3n esp%C3%ADn-%C3%B3rbita"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Interacción espín-órbita — La interacción espín órbita, en magnetoquímica, es la interacción magnética(cuántica) entre el momento magnético de espín y el momento magnético orbital. El acoplamiento espín órbita es el acoplamiento entre estos momentos magnéticos. Sólo lo… …   Enciclopedia Universal

  • Acoplamiento espín-órbita — Saltar a navegación, búsqueda Interacción espín órbita Obtenido de Acoplamiento esp%C3%ADn %C3%B3rbita …   Wikipedia Español

  • Interacción de canje — Dos orbitales d de iones metálicos vecinos: la interacción de canje J se produce entre dos electrones con el mismo número cuántico de espín Ms, e impide que …   Wikipedia Español

  • Acoplamiento de momento angular — En mecánica cuántica, el procedimiento de construir estados propios del momento angular total (estados de un sistema con valores bien definidos del momento angular) a partir de los estados propios de los momentos angulares individuales se llama… …   Wikipedia Español

  • Átomo de hidrógeno — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… …   Wikipedia Español

  • Mn12 — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… …   Wikipedia Español

  • Ecuación de Dirac — Saltar a navegación, búsqueda La ecuación de Dirac de ondas relativista de la mecánica cuántica fue formulada por Paul Dirac en 1928. Da una descripción de las partículas elementales de espín ½, como el electrón, y es completamente consistente… …   Wikipedia Español

  • Anisotropía en el canje magnético — Saltar a navegación, búsqueda La anisotropía magnética es la no homogeneidad de las propiedades magnéticas (como la susceptibilidad magnética) al ser medidas en diferentes direcciones del espacio. Decimos que un sistema presenta canje magnético… …   Wikipedia Español

  • Desdoblamiento a campo nulo — Saltar a navegación, búsqueda El desdoblamiento a campo nulo o desdoblamiento a campo cero D, en magnetoquímica, es la diferencia de energía que separa, sin campo magnético aplicado y dentro de un mismo número cuántico de espín S, a los estados… …   Wikipedia Español

  • Hamiltoniano (mecánica cuántica) — El Hamiltoniano H tiene dos significados distintos, aunque relacionados. En mecánica clásica, es una función que describe el estado de un sistema mecánico en términos de variables posición y momento, y es la base para la reformulación de la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”