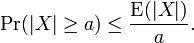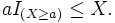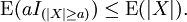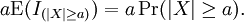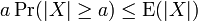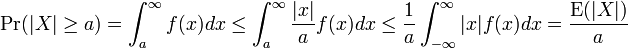Desigualdad de Márkov

Desigualdad de Márkov

Desigualdad de Márkov

En teoría de la probabilidad, la desigualdad de Márkov proporciona una cota superior para la probabilidad de que una función no negativa de una variable aleatoria sea mayor o igual que una constante positiva. Su nombre le viene del matemático ruso Andréi Márkov.

La desigualdad de Márkov relaciona las probabilidades con la esperanza matemática y proporciona cotas útiles -aunque habitualmente poco ajustadas- para la función de distribución de una variable aleatoria.


Teorema

La desigualdad de Márkov afirma que si X es una variable aleatoria cualquiera y a > 0, entonces

\textrm{Pr}(|X| \geq a) \leq \frac{\textrm{E}(|X|)}{a}.

Prueba

Para cualquier suceso A, sea IA la variable aleatoria indicatriz de A, esto es, IA = 1 si ocurre A y es 0 en el caso contrario. Entonces

aI_{(X \geq a)} \leq X.\,

Por lo tanto

\operatorname{E}(aI_{(|X| \geq a)}) \leq \operatorname{E}(|X|).\,

Ahora, nótese que el lado izquierdo de esta desigualdad coincide con

a\operatorname{E}(I_{(|X| \geq a)})=a\Pr(|X| \geq a).\,

Por lo tanto tenemos

a\Pr(|X| \geq a) \leq \operatorname{E}(|X|)\,

y como a > 0, se pueden dividir ambos lados entre a.

Prueba alternativa

Una prueba más formal, relacionada con el análisis real, es la siguiente:

\Pr(|X| \geq a) = \int_a^\infty {f(x)dx} \leq \int_a^\infty {\frac{|x|}{a}f(x)dx} \leq \frac{1}{a} \int_{-\infty}^{\infty}{|x|f(x)dx} = \frac{\operatorname{E}(|X|)}{a}

En la introducción de 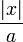\frac{|x|}{a} , nótese que ya que estamos considerando la variable aleatoria sólo en sus valores iguales o mayores a a, 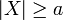|X| \geq a y, por tanto, 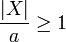\frac{|X|}{a} \geq 1 , con lo que al multiplicar f(x)dx por algo mayor a uno será igual o mayor. La segunda desigualdad viene de añadir la suma 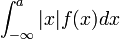\int_{-\infty}^a {|x|f(x)dx} , que siempre será positiva ya que se integra algo positivo como es el valor absoluto (por :f(x) que es positiva).


Obtenido de "Desigualdad de M%C3%A1rkov"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Desigualdad de Markov — En teoría de la probabilidad, la desigualdad de Markov proporciona una cota superior para la probabilidad de que una función no negativa de una variable aleatoria sea mayor o igual que una constante positiva. Su nombre le viene del matemático… …   Enciclopedia Universal

  • Desigualdad de Chebyshov — Saltar a navegación, búsqueda En probabilidad, la desigualdad de Chebyshov es un resultado estadístico que ofrece una cota inferior a la probabilidad de que el valor de una variable aleatoria con varianza finita esté a una cierta distancia de su… …   Wikipedia Español

  • Andréi Márkov — Andréi Márkov. Andréi Andréyevich Márkov (Андрей Андреевич Марков) (14 de junio de 1856 20 de julio de 1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades. Márkov nació en Riazán, Rusia …   Wikipedia Español

  • Función indicatriz — Gráfico de una función indicatríz que muestra a un subconjunto de los puntos de un cuadrado (en rojo), donde los puntos tienen coordenada z=1 (color ocre), mientras que los puntos del cuadrado …   Wikipedia Español

  • Pafnuti Chebyshov — Pafnuti Lvóvich Chebyshov. Pafnuti Lvóvich Chebyshov (Пафнутий Львович Чебышёв) (16 de mayo de 1821 8 de diciembre de 1894) fue un matemático ruso. Su nombre se translitera también como Tchebychev, Tchebycheff, Tschebyscheff, Chebyshev o Čebišëv …   Wikipedia Español

  • Robert Solow — Saltar a navegación, búsqueda Robert Solow Robert Merton Solow (23 de agosto de 1924, Nueva York, EE. UU.) es un economista norteamericano especialmente conocido por sus trabajos sobre teoría del crecimiento económico. En 1987 recibió el Premio… …   Wikipedia Español

  • Pafnuty Chebyshev — Pafnuty Lvóvich Chebyshev (Пафнутий Львович Чебышёв) (1821 1894) fue un matemático ruso. Su nombre se translitera también como Tchebychev, Tchebycheff, Tschebyscheff o Čebišev. Fue maestro de Andrei Markov. Es conocido por su trabajo en el área… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”