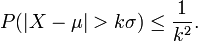En probabilidad, la desigualdad de Chebyshov es un resultado estadístico que ofrece una cota inferior a la probabilidad de que el valor de una variable aleatoria con varianza finita esté a una cierta distancia de su esperanza matemática o de su media; equivalentemente, el teorema proporciona una cota superior a la probabilidad de que los valores caigan fuera de esa distancia respecto de la media. El teorema es aplicable incluso en distribuciones que no tienen forma de "curva de campana" y acota la cantidad de datos que están o no "en medio".

Teorema: Sea X una variable aleatoria de media μ y varianza finita σ². Entonces, para todo número real k > 0,

Sólo los casos con k > 1 proporcionan información útil.

Para ilustrar este resultado, supongamos que los artículos de Wikipedia tienen una extensión media de 1000 caracteres y una desviación típica de 200 caracteres. De la desigualdad de Chebyshov se deduce que al menos el 75% de los artículos tendrán una extensión comprendida entre 600 y 1400 caracteres (k = 2).

Otra consecuencia del teorema es que para cada distribución de media μ y desviación típica finita σ, al menos la mitad de los valores caerán en el intervalo (μ-√2 σ, μ+√2 σ).

Las cotas proporcionadas por la desigualdad de Chebyshov, en general, no se pueden mejorar; es posible construir una variable aleatoria cuyas cotas de Chebyshov sean exactamente iguales a las probabilidades reales. Sin embargo, en general el teorema proporcionará cotas poco precisas.

El teorema puede ser útil a pesar de las cotas imprecisas porque se aplica a una amplia gama de variables que incluye las que están muy alejadas de la distribución normal, y porque las cotas son fáciles de calcular. El teorema se emplea para demostrar la ley débil de los números grandes.

El teorema recibe su nombre del matemático Pafnuti Chebyshov.

Véase también

• Desigualdad de Márkov.