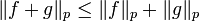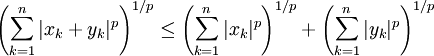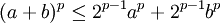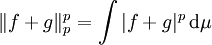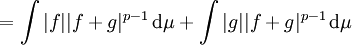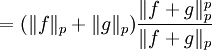Desigualdad de Minkowski

Saltar a navegación, búsqueda

En analisis matematico, la desigualdad de Minkowski establece que los espacios L^p son espacios vectoriales con una norma. Sea S un espacio medible, sea 1 ≤ p ≤ ∞ y sea f y g elementos de L^p(S). Entonces f + g es de L^p(S), y es tiene

$\|f+g\|_p \le \|f\|_p + \|g\|_p$

con la igualdad para el caso1 < p < ∞ si y sólo si f y g son positivamente linealmente dependientes (que significa que f = $λ$ g o g = $λ$ f para algun $λ$ ≥ 0).

La desigualdad de Minkowski es la desigualdad: triangular en L^p(S).

Igual que la desigualdad de Hölder, la desigualdad de Minkowski se puede especificar para sucesiones y vectores haciendo:

$\left( \sum_{k=1}^n |x_k + y_k|^p \right)^{1/p} \le \left( \sum_{k=1}^n |x_k|^p \right)^{1/p} + \left( \sum_{k=1}^n |y_k|^p \right)^{1/p}$

para todos los números reales (o complejos) x₁, ..., x_n, y₁, ..., y_n y donde n es el cardinal de S (el número de elementos de S).

Demostración

Primero se demuestra que f+g tiene una p-norma finita sobre f y g ambas la tienen , esto se sigue de,

$|f + g|^p \le 2^{p-1}(|f|^p + |g|^p)$

En efecto, aquí se hace servir el hecho de que $h (x) = x p$ es una funcion convexa sobre 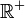$\mathbb{R}^+$ (para $p$ mas grande que 1) y por lo tanto, si a y b son positivos entonces,

$\left(\frac{1}{2} a + \frac{1}{2} b\right)^p \le \frac{1}{2}a^p + \frac{1}{2} b^p$

Lo cual significa que,

$(a+b)^p \le 2^{p-1}a^p + 2^{p-1}b^p$

Ahora, se puede hablar legítimamente de 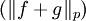$(\|f + g\|_p)$ . Si es zero, entonces se cumple la desigualdad de Minkowski. ahora , suponinedo que 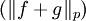$(\|f + g\|_p)$ no es zero. haciendo servir la desigualdad de Hölder

$\|f + g\|_p^p = \int |f + g|^p \, \mathrm{d}\mu$

$\le \int (|f| + |g|)|f + g|^{p-1} \, \mathrm{d}\mu$

$=\int |f||f + g|^{p-1} \, \mathrm{d}\mu+\int |g||f + g|^{p-1} \, \mathrm{d}\mu$

$\stackrel{\text{H}\ddot{\text{o}}\text{lder}}{\le} \left( \left(\int |f|^p \, \mathrm{d}\mu\right)^{1/p} + \left (\int |g|^p \,\mathrm{d}\mu\right)^{1/p} \right) \left(\int |f + g|^{(p-1)\left(\frac{p}{p-1}\right)} \, \mathrm{d}\mu \right)^{1-\frac{1}{p}}$

$= (\|f\|_p + \|g\|_p)\frac{\|f + g\|_p^p}{\|f + g\|_p}$

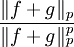Se obtiene la desigualdad de Minkowski multiplicando por ambos lados $\frac{\|f + g\|_p}{\|f + g\|_p^p}$ .

Referencias

Hardy, G., Littlewood J.E., Polya, G. (1999). Inequalities, Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8
H. Minkowski, Geometrie der Zahlen , Chelsea, reprint (1953)
M.I. Voitsekhovskii (2001), "Minkowski inequality", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1-55608-010-4

Obtenido de "Desigualdad de Minkowski"

Categoría: Desigualdades

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Suma de Minkowski — En geometría, la suma de Minkowski es una operación sobre las partes de un espacio vectorial. A dos partes A y B asocia su conjunto suma, formado por la suma de los elementos de A y B: La suma de dos compactos es compacta, así es posible… … Wikipedia Español
Integración — La integral definida de una función representa el área limitada por la gráfica de la función, con signo positivo cuando la función toma valores positivos y negativo cuando toma valores negativos. Para otros usos de este término, véase Integración … Wikipedia Español
Teoría relativista de la gravitación — La teoría relativista de la gravitación (TRG) es una teoría del campo gravitatorio formulada, por Logunov, Mestvirishvili y Petrov. Dicha teoría construye una teoría del campo gravitatorio dentro de los límites de la teoría especial de la… … Wikipedia Español
Teoremas fundamentales de la economía del bienestar — Hay dos teoremas fundamentales de la economía del bienestar.[1] [2] El primero afirma que cualquier equilibrio competitivo o walrasiano[3] lleva a una situación de asignación de recursos económicos que es eficiente de acuerdo a Pareto. El segundo … Wikipedia Español
Hermann Weyl — Hermann Klaus Hugo Weyl Hermann Weyl (izquierda) y Ernst Peschl (derecha) Nacimiento 9 de noviembre 1885 Elmshorn … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Desigualdad de Minkowski

Desigualdad de Minkowski

Demostración

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Desigualdad de Minkowski

Desigualdad de Minkowski

Demostración

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo